题目内容
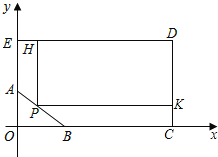
【题目】如图,四边形ABCD是矩形,点A在第四象限y1=﹣![]() 的图象上,点B在第一象限y2=
的图象上,点B在第一象限y2=![]() 的图象上,AB交x轴于点E,点C与点D在y轴上,AD=
的图象上,AB交x轴于点E,点C与点D在y轴上,AD=![]() ,S矩形OCBE=
,S矩形OCBE=![]() S矩形ODAE.
S矩形ODAE.
(1)求点B的坐标.
(2)若点P在x轴上,S△BPE=3,求直线BP的解析式.

【答案】(1)B(![]() ,2);(2)直线BP的解析式是y=
,2);(2)直线BP的解析式是y=![]() x+1或y=﹣
x+1或y=﹣![]() x+3.
x+3.
【解析】
(1)根据反比例函数系数k的几何意义求得k=3,得出![]() ,由题意可知B的横坐标为
,由题意可知B的横坐标为![]() ,代入即可求得B的坐标;
,代入即可求得B的坐标;
(2)设P(a,0),根据三角形面积求得P的坐标,然后根据待定系数法即可求得直线BP的解析式.
(1)∵S矩形OCBE=![]() S矩形ODAE,点B在第一象限y2=
S矩形ODAE,点B在第一象限y2=![]() 的图象上,
的图象上,
∵点A在第四象限y1=﹣![]() 的图象上,
的图象上,
∴S矩形ODEA=2
∴S矩形OCBE=![]() ×2=3,
×2=3,
∴k=3,
∴y2=![]() ,
,
∵OE=AD=![]() ,
,
∴B的横坐标为![]() ,
,
代入y2=![]() 得,y=
得,y=![]() =2,
=2,
∴B(![]() ,2);
,2);
(2)设P(a,0),
∵S△BPE=![]() PEBE=
PEBE=![]() ,
,
解得a=﹣![]() 或
或![]() ,
,
∴点P(﹣![]() ,0)或(
,0)或(![]() ,0),
,0),
设直线BP的解析式为y=mx+n(m≠0),
①若直线过(![]() ,2),(﹣
,2),(﹣![]() ,0),
,0),
则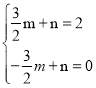 ,解得
,解得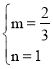 ,
,
∴直线BP的解析式为y=![]() x+1;
x+1;
②若直线过(![]() ,2),(
,2),(![]() ,0),
,0),
则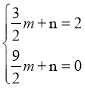 ,解得
,解得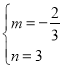 ,
,
∴直线BP的解析式为y=﹣![]() x+3;
x+3;
综上,直线BP的解析式是y=![]() x+1或y=﹣
x+1或y=﹣![]() x+3.
x+3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目