题目内容
如图，二次函数y=ax2+bx+3的图象经过点A（-1，0），B（3，0），那么一元二次方程ax2+bx+3=0的根是考点：抛物线与x轴的交点
专题：
分析：利用二次函数图象与x轴交点即为y=0时，x的值，进而得出一元二次方程的根．
解答：解：∵二次函数y=ax2+bx+3的图象经过点A（-1，0），B（3，0），
∴一元二次方程ax2+bx+3=0的根是：x1=-1，x2=3．
故答案为：x1=-1，x2=3．
∴一元二次方程ax2+bx+3=0的根是：x1=-1，x2=3．
故答案为：x1=-1，x2=3．
点评：此题主要考查了抛物线与x轴的交点，利用y=0时求出x的值是解题关键．
练习册系列答案
相关题目
如图，直线L：y=-x+3与两坐标轴分别相交于点A、B．数轴上点A表示的数是-1，将点A沿数轴移动2个单位到点B，则点B所表示的数是（ ）
| A、-3 | B、1 |
| C、-1或3 | D、-3或1 |
在下面四个说法中正确的有（ ）
①互为相反数的两个数的绝对值相等 ②正数的绝对值等于它本身
③一个数的倒数等于它本身，这个数是±1 ④没有最大的整数
⑤几个有理数相乘，如果负因数有奇数个，则积为负数．
①互为相反数的两个数的绝对值相等 ②正数的绝对值等于它本身
③一个数的倒数等于它本身，这个数是±1 ④没有最大的整数
⑤几个有理数相乘，如果负因数有奇数个，则积为负数．
| A、1个 | B、2个 | C、3个 | D、4个 |
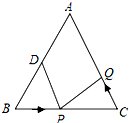如图，已知△ABC中，AB=AC=20cm，∠ABC=∠ACB，BC=16cm，点D是AB的中点．点P在线段BC上以6厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动，且点Q的运动速度与点P的运动速度相等．经过1秒后，△BPD与△CQP是否全等，请说明理由．