题目内容
有n个数,第一个记为a1,第二个记为a2,…,第n个记为an,若a1=
,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”.
(1)求a2,a3,a4的值;
(2)根据(1)的计算结果,请你猜想并写出a2009,a2010的值;
(3)计算:a1×a2×a3×…×a2009×a2010×a2011=.
| 1 |
| 2 |
(1)求a2,a3,a4的值;
(2)根据(1)的计算结果,请你猜想并写出a2009,a2010的值;
(3)计算:a1×a2×a3×…×a2009×a2010×a2011=.
考点:规律型:数字的变化类,倒数
专题:
分析:(1)首先根据已知求得a2,a3,a4的值即可;
(2)(3)由上面的结果,然后找到这组数的循环规律即可求解.
(2)(3)由上面的结果,然后找到这组数的循环规律即可求解.
解答:解:(1)a2=
=2,
a3=
=-1;
a4=
=
,
(2)由上面计算得出:
每3个数循环一次.
2009÷3=669…2,
则a2009=a2=2,
2010÷3=670,
则a2010=a3=-1.
(3)a1×a2×a3×…×a2009×a2010×a2011=
=2×(-1)×
×…×2×(-1)×
×2
=2.
| 1 | ||
1-
|
a3=
| 1 |
| 1-2 |
a4=
| 1 |
| 1-(-1) |
| 1 |
| 2 |
(2)由上面计算得出:
每3个数循环一次.
2009÷3=669…2,
则a2009=a2=2,
2010÷3=670,
则a2010=a3=-1.
(3)a1×a2×a3×…×a2009×a2010×a2011=
=2×(-1)×
| 1 |
| 2 |
| 1 |
| 2 |
=2.
点评:此题考查了数字的变化规律,正确找到循环关系是解题关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
满足不等式
<x<
的整数x共有( )个.
| 4 | ||||
|
| 4 | ||||
|
| A、4 | B、5 | C、6 | D、7 |
抛物线y=-x2+4x-1的顶点坐标是( )
| A、(-2,3) |
| B、(2,3) |
| C、(2,-3) |
| D、(-2,-3) |
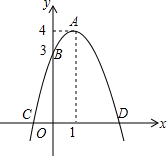 如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.
如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点. 如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx+3=0的根是
如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx+3=0的根是