题目内容
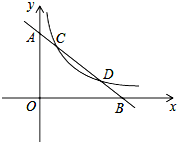 如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.
如图,直线L:y=-x+3与两坐标轴分别相交于点A、B.(1)当反比例函数y=
| k |
| x |
(2)若反比例函数y=
| k |
| x |
| 2 |
(3)在(2)的条件下,请你直接写出关于x的不等式-x+3<
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据反比例函数y=
(k>0,x>0)的图象在第一象限内与直线L总有公共点,得判别式大于或等于0,可得答案;
(2)根据韦达定理,可得方程两根的关系,根据两点间距离公式,可得答案;
(3)反比例函数图象落在直线上方的部分对应的x的取值范围,即为所求.
| k |
| x |
(2)根据韦达定理,可得方程两根的关系,根据两点间距离公式,可得答案;
(3)反比例函数图象落在直线上方的部分对应的x的取值范围,即为所求.
解答:解:(1)当反比例函数y=
(k>0,x>0)的图象在第一象限内与直线L总有公共点时,得-x+3=
,
整理得:x2-3x+k=0,
△=(-3)2-4k≥0,
解得k≤
.
即k的取值范围为:0<k≤
;
(2)∵x2-3x+k=0,
设该方程的两根是x1、x2.
∴x1+x2=3,x1•x2=k,
∵CD=
=2
,
∴2[(x1+x2)2-4x1•x2]=8,
即 2(9-4k)=8,
解得 k=
;
(3)当k=
时,x2-3x+k=0,
解得x1=
,x2=
,
由反比例函数图象在直线上方的区域得0<x<
或x>
.
| k |
| x |
| k |
| x |
整理得:x2-3x+k=0,
△=(-3)2-4k≥0,
解得k≤
| 9 |
| 4 |
即k的取值范围为:0<k≤
| 9 |
| 4 |
(2)∵x2-3x+k=0,
设该方程的两根是x1、x2.
∴x1+x2=3,x1•x2=k,
∵CD=
| (x1-x2)2+(y1-y2)2 |
| 2 |
∴2[(x1+x2)2-4x1•x2]=8,
即 2(9-4k)=8,
解得 k=
| 5 |
| 4 |
(3)当k=
| 5 |
| 4 |
解得x1=
| 1 |
| 2 |
| 5 |
| 2 |
由反比例函数图象在直线上方的区域得0<x<
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题,利用了韦达定理,两点间的距离公式,一次函数与不等式的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx+3=0的根是
如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx+3=0的根是