题目内容
12.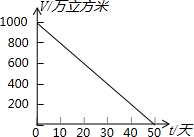 2007年的夏天,湖南省由于持续高温和连日无雨,水库蓄水量普遍下降,如图是某水库的蓄水量V(万立方米)与干旱持续时间t(天)之间的关系图,请根据此图,回答下列问题:
2007年的夏天,湖南省由于持续高温和连日无雨,水库蓄水量普遍下降,如图是某水库的蓄水量V(万立方米)与干旱持续时间t(天)之间的关系图,请根据此图,回答下列问题:(1)该水库原蓄水量为多少万立方米?持续干旱10天后,水库蓄水量为多少万立方米?
(2)若水库的蓄水量小于400万立方米时,将发出严重干旱警报,请问持续干旱多少天后,将发出严重干旱警报?
(3)按此规律,持续干旱多少天时,水库将干涸?
分析 (1)原蓄水量即t=0时v的值,持续干旱10天后的蓄水量即t=10时v的值;
(2)即找到v=400时,相对应的t的值;
(3)从第10天到第30天,水库下降了800-400=400万立方米,一天下降$\frac{400}{30-10}$=20万立方米,第30天的400万立方米还能用$\frac{400}{20}$=20天,即50天时干涸.
解答 解:(1)当t=0时,v=1000∴水库原蓄水量为1000万米3,
当t=10时,v=800,
∴水库原蓄水量为1 000万立方米,持续干旱10天后,蓄水量为800万立方米.
(2)当v=400时,t=30,∴持续干旱30天后将发出严重干旱警报.
(3)从第10天到第30天,水库下降了(800-400)万立方米,一天下降$\frac{400}{30-10}$=20万立方米,
故根据此规律可求出:30+$\frac{400}{20}$=50天,那么持续干旱50天后水库将干涸.
点评 此题考查函数图象问题,解决本题的关键是正确理解函数图象横纵坐标表示的意义,理解问题的过程,得到相应的点的意义.

练习册系列答案
相关题目
2.sin60°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
 如图,小明把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,他发现2∠A=∠1+∠2,你能帮他解释其中的原因吗?
如图,小明把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,他发现2∠A=∠1+∠2,你能帮他解释其中的原因吗?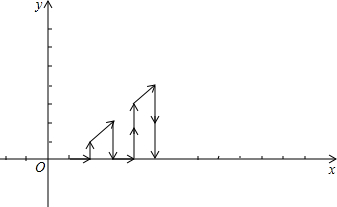 如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).
如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3). 某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升7.09元.
某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升7.09元. 如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长交AB于点E,连接BP并延长交AD于点F,交CD延长线于点G.
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长交AB于点E,连接BP并延长交AD于点F,交CD延长线于点G.