题目内容
三角形的面积R=12cm2,周长L=24cm,则其内切圆的半径为 cm.
考点:三角形的内切圆与内心
专题:计算题
分析:根据公式S=
r(a+b+c)(r为三角形内切圆的半径,a、b、c为三角形三边的长)求解.
| 1 |
| 2 |
解答:解:∵S=
r(a+b+c)(r为三角形内切圆的半径,a、b、c为三角形三边的长),
∴r=
=1(cm),
即三角形内切圆的半径为1cm.
故答案为1.
| 1 |
| 2 |
∴r=
| 12×2 |
| 24 |
即三角形内切圆的半径为1cm.
故答案为1.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.记住三角形面积公式S=
r(a+b+c)(r为三角形内切圆的半径,a、b、c为三角形三边的长.
| 1 |
| 2 |

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 如图,菱形ABCD,AB=17,BD=16,延长BD至点E,使AE=25,连接AE,则DE的长为( )
如图,菱形ABCD,AB=17,BD=16,延长BD至点E,使AE=25,连接AE,则DE的长为( )| A、8 | B、9 | C、11 | D、12 |
八年级一班的数学老师王金华老师要选拔一名同学参加全区的素质教育抽测.甲、乙两名同学在相同的条件下,各经过4次单元测试,经过计算,甲、乙测试的平均成绩都是82分,甲的方差是2.2,乙的方差是2.8,下列说法不一定正确的是( )
| A、甲、乙两人的总分相同 |
| B、甲、乙的众数相同 |
| C、乙的成绩波动大 |
| D、甲的成绩波动大 |
函数y=2x+b的图象与两坐标轴围成的三角形的面积为4,则函数的表达式为( )
| A、y=2x+4 |
| B、y=2x-4 |
| C、y=2x+4或 y=2x-4 |
| D、y=-2x-4 |
在实数-
,0.
,
,
,0.1010010001,
中,无理数的个数为( )
| 5 |
| • |
| 2 |
| • |
| 1 |
| π |
| 3 |
| 22 |
| 7 |
| 3 | 8 |
| A、1个 | B、2个 | C、3个 | D、4个 |
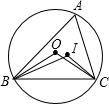 如图,△ABC中,O为△ABC的外心,I为△ABC的内心,设∠BOC=y1°,∠BIC=y2°,∠A=x°(∠BOC≤180°).
如图,△ABC中,O为△ABC的外心,I为△ABC的内心,设∠BOC=y1°,∠BIC=y2°,∠A=x°(∠BOC≤180°).