题目内容
 如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=| 1 |
| 2 |
(1)求点C的坐标;
(2)若点D在反比例函数y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据正切值,可得PD的斜率,根据直线垂直,可得BD的斜率,可得直线BC,根据函数值为0,可得C点坐标;
(2)根据自变量的值,可得D点坐标,根据待定系数法,可得函数解析式.
(2)根据自变量的值,可得D点坐标,根据待定系数法,可得函数解析式.
解答:解:Rt△PBD的斜边PB落在y轴上,
∴BD⊥PD,
kPD=cot∠BPD=
=2,
kBD•kPD=-1,
kBD=-
,
直线BD的解析式是y=-
x+3,
当y=0时,-
x+3=0,
x=6,
C点坐标是(6,0);
(2)当x=4时,y=-
×4+3=1,
∴D(4,1).
点D在反比例函数y=
(k>0)的图象上,
∴k=4×1=4,
∴反比例函数的解析式为 y=
.
∴BD⊥PD,
kPD=cot∠BPD=
| 1 |
| tan∠BPD |
kBD•kPD=-1,
kBD=-
| 1 |
| 2 |
直线BD的解析式是y=-
| 1 |
| 2 |
当y=0时,-
| 1 |
| 2 |
x=6,
C点坐标是(6,0);
(2)当x=4时,y=-
| 1 |
| 2 |
∴D(4,1).
点D在反比例函数y=
| k |
| x |
∴k=4×1=4,
∴反比例函数的解析式为 y=
| 4 |
| x |
点评:本题考查了反比例函数与一次函数的交点问题,先求出PD的斜率求出BD的斜率,求出直线BD,再求出点的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
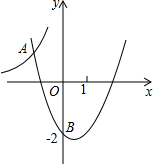 如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-
如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-| 8 |
| x |
| A、y=x2-x-2 |
| B、y=x2-x+2 |
| C、y=x2+x-2 |
| D、y=x2+x+2 |
 如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则
如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则