题目内容
边长为10、10、12的三角形的外心与重心之间的距离为 .
考点:三角形的外接圆与外心,三角形的重心
专题:计算题
分析:如图,AB=AC=10,BC=12,作AD⊥BC于D,则BD=CD=
BC=6,根据三角形外心与重心的定义可得到△ABC的外心O、重心G都在AD上,连结OB,设三角形的外接圆半径为r,根据外心的性质得OB=OA=r,接着利用勾股定理,在Rt△ABD中计算出AD=8,在Rt△ODB中得到(8-r)2+62=r2,解得r=
,则OD=AD-OA=
,再根据重心的性质得到GD=
AD=
,所以OG=GD-OD=
.
| 1 |
| 2 |
| 25 |
| 4 |
| 7 |
| 4 |
| 1 |
| 3 |
| 8 |
| 3 |
| 11 |
| 12 |
解答:解:如图, AB=AC=10,BC=12,
AB=AC=10,BC=12,
作AD⊥BC于D,则BD=CD=
BC=6,所以△ABC的外心O、重心G都在AD上,
连结OB,设三角形的外接圆半径为r,则OB=OA=r,
在Rt△ABD中,∵AB=10,BD=6,
∴AD=
=8,
在Rt△ODB中,∵OD2+BD2=OB2,
∴(8-r)2+62=r2,解得r=
,
∴OD=AD-OA=8-
=
,
∵点G为△ABC的重心,
∴GD=
AD=
,
∴OG=GD-OD=
-
=
,
即三角形的外心与重心之间的距离为
.
故答案为
.
 AB=AC=10,BC=12,
AB=AC=10,BC=12,作AD⊥BC于D,则BD=CD=
| 1 |
| 2 |
连结OB,设三角形的外接圆半径为r,则OB=OA=r,
在Rt△ABD中,∵AB=10,BD=6,
∴AD=
| AB2-BD2 |
在Rt△ODB中,∵OD2+BD2=OB2,
∴(8-r)2+62=r2,解得r=
| 25 |
| 4 |
∴OD=AD-OA=8-
| 25 |
| 4 |
| 7 |
| 4 |
∵点G为△ABC的重心,
∴GD=
| 1 |
| 3 |
| 8 |
| 3 |
∴OG=GD-OD=
| 8 |
| 3 |
| 7 |
| 4 |
| 11 |
| 12 |
即三角形的外心与重心之间的距离为
| 11 |
| 12 |
故答案为
| 11 |
| 12 |
点评:本题考查了三角形的外接圆与外心:三角形外心到三角形三个顶点的距离相等.也考查了三角形重心的性质(三角形重心把三角形中线三等份).

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
下列判断正确的是( )
| A、近似数0.380是精确到0.01 |
| B、近似数5.6万是精确到十分位 |
| C、近似数300是精确到百位 |
| D、近似数1.60×103是精确到十位 |
 两个长方形重叠部分的面积相当于大长方形的
两个长方形重叠部分的面积相当于大长方形的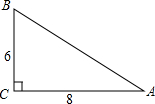 某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长分别为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边长的直角三角形.请你设计出所有合适的方案,画出草图,并求出扩建后的等腰三角形花圃的面积.
某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长分别为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边长的直角三角形.请你设计出所有合适的方案,画出草图,并求出扩建后的等腰三角形花圃的面积.