题目内容
2.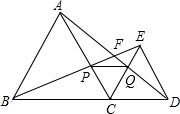 如图,在线段BD上取一点C,以BC,CD为边分别作正三角形ABC和正三角形ECD,连结AD,交EC于点Q,连结BE,交AC于点P,交AD于点F.
如图,在线段BD上取一点C,以BC,CD为边分别作正三角形ABC和正三角形ECD,连结AD,交EC于点Q,连结BE,交AC于点P,交AD于点F.(1)通过旋转,图中可得到哪些全等三角形?
(2)求∠BFD的度数;
(3)PQ与BD平行吗?若平行,请说明理由.
分析 (1)通过旋转,图中可得到△ACD≌△BCE,△BPC≌△AQC,△PCE≌△QCD;
(2)根据∠BFD=∠BED+∠ADE,又∠BEC=∠ADC,可得∠BFD=∠CED+∠CDE=120°;
(3)由△BPC≌△AQC,得到CP=CQ,根据∠PCQ=60°,所以△PCQ为正三角形,进而得到∠APQ=∠ACQ+∠CQP=120°,又由∠ACD=∠ACQ+∠ECD=120°,所以∠APQ=∠ACD,即可得到PQ‖CD.
解答 解:(1)通过旋转,图中可得到△ACD≌△BCE,△BPC≌△AQC,△PCE≌△QCD;
(2)∵∠BFD=∠BED+∠ADE,又∠BEC=∠ADC,
∴∠BFD=∠CED+∠CDE=120°;
(3)∵△BPC≌△AQC,
∴CP=CQ,
∵∠PCQ=60°,
∴△PCQ为正三角形,
∴∠APQ=∠ACQ+∠CQP=120°,
∵∠ACD=∠ACQ+∠ECD=120°,
∴∠APQ=∠ACD,
∴PQ‖CD.
点评 本题考查了全等三角形的性质与判定、等边三角形的性质,解决本题的关键是证明三角形全等,利用全等三角形得到相等的边.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
7.已知A=3m2-7m+5,B=-3m2-7m-7,则B-A一定( )
| A. | 大于0 | B. | 等于-12或-6 | C. | 小于0 | D. | 最大值为12 |
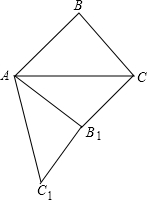 如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2.
如图,在△ABC中,∠ABC=90°,AB=5,BC=4,将△ABC绕顶点A旋转到△AB1C1的位置(其中点B1对应点B,点C1对应点C),使得B1C∥AB,那么B1C=2. 如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有AB=DE,BC=EF,BF=CE..
如图,∠B=∠E=90°,AC=DF,BF=EC,则除条件以外,相等的线段还有AB=DE,BC=EF,BF=CE..