题目内容
17. 如图,在△ABC中,点D,E分别在AC,AB上且DE∥BC,若S△ADE:S△BDE=2:3,则S△ADE:S△ACB=( )
如图,在△ABC中,点D,E分别在AC,AB上且DE∥BC,若S△ADE:S△BDE=2:3,则S△ADE:S△ACB=( )| A. | 2:3 | B. | 4:9 | C. | 4:25 | D. | 4:19 |
分析 根据题意可以求得△ADE和△ACB的相似比,从而可以求得两个三角形的面积之比,本题得以解决.
解答 解:∵S△ADE:S△BDE=2:3,DE∥BC,设点A到DE的距离为a,点E到BC的距离为b,
∴$\frac{DE•a}{2}:\frac{DE•b}{2}=2:3$,
∴a:b=2:3,
∴点A到DE的距离与点A到BC的距离的比值是2:5,
∴$\frac{{S}_{△ADE}}{{S}_{△ACB}}=(\frac{2}{5})^{2}=\frac{4}{25}$,
故选C.
点评 本题考查相似三角形的判定与性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
8. 如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )
如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )
 如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )
如图,在平面直角坐标系中,AD平分∠OAB,DB⊥AB,BC∥OA,若点B的横坐标为1,点D的坐标为(0,$\sqrt{3}$),则点C的坐标是( )| A. | (0,2) | B. | (0,5) | C. | (0,$\sqrt{5}$) | D. | (0,$\sqrt{3}$+$\sqrt{2}$) |
5.在$\sqrt{6}$、$\frac{2}{3}$、1.8、$\frac{π}{4}$这4个数中,有理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.必然事件的概率是( )
| A. | 1 | B. | 0 | C. | 大于0且小于1 | D. | 大于1 |
2. 如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( )
如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( )
 如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( )
如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( )| A. | 50° | B. | 60° | C. | 70° | D. | 70° |
9.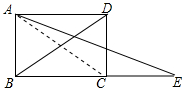 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )
如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )
 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )
如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E的度数是( )| A. | 45° | B. | 30° | C. | 20° | D. | 15° |
6. 如图,在扇形统计图中,若整个圆表示麦田9亩,则扇形C表示麦田是( )
如图,在扇形统计图中,若整个圆表示麦田9亩,则扇形C表示麦田是( )
 如图,在扇形统计图中,若整个圆表示麦田9亩,则扇形C表示麦田是( )
如图,在扇形统计图中,若整个圆表示麦田9亩,则扇形C表示麦田是( )| A. | 2.25亩 | B. | 2.97亩 | C. | 3.78亩 | D. | 9亩 |
7.若二次根式$\sqrt{x-2}$有意义,则 x 的取值范围为( )
| A. | x>2 | B. | x<2 | C. | x≤2 | D. | x≥2 |
 如图,数轴上有A、B、C、D四个整数点(即各点均表示整数),且3AB=BC=2CD.若A、D两点所表示的数分别是-6和5,则线段AC的中点所表示的数是( )
如图,数轴上有A、B、C、D四个整数点(即各点均表示整数),且3AB=BC=2CD.若A、D两点所表示的数分别是-6和5,则线段AC的中点所表示的数是( )