题目内容
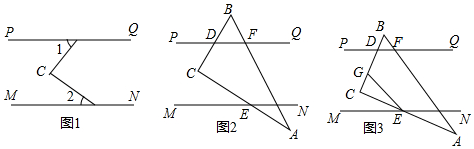
17.某班开展勤俭节约的活动,对每个同学的一天的消费情况进行调查,得到统计图如图所示:
(1)求该班的总人数;
(2)将条形图补充完整,并写出消费金额的中位数;
(3)该班这一天平均每人消费多少元?
分析 (1)根据C有14人,占28%,即可求得该班的总人数;
(2)根据(1)中的答案可以求得消费10元的人数,从而可以将条形统计图补充完整,进而求得消费金额的中位数;
(3)根据加权平均数的计算方法可以求得该班这一天平均每人消费的金额.
解答 解:(1)由题意可得,
该班的总人数为:14÷28%=50,
即该班的总人数是50;
(2)消费10元的有:50-9-14-7-4=16(人),
补充完整的统计图如右图所示,
消费金额的中位数是:$\frac{10+15}{3}=12.5$;
(3)由题意可得,
该班这一天平均每人消费:$\frac{9×5+16×10+14×15+7×20+4×25}{50}$=13.1(元),
即该班这一天平均每人消费13.1元.
点评 本题考查条形统计图、扇形统计图、中位数、加权平均数,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.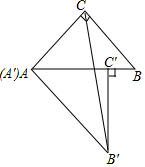 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )| A. | 3$\sqrt{3}$ | B. | 6 | C. | 3$\sqrt{2}$ | D. | $\sqrt{21}$ |
2.下列事件中,是必然事件的是( )
| A. | 将油滴入水中,油会浮在水面上 | |
| B. | 车辆随机到达一个路口,遇到红灯 | |
| C. | 如果a2=b2,那么a=b | |
| D. | 掷一枚质地均匀的硬币,一定正面向上 |
6.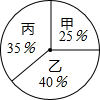 某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率如扇形统计图所示(没有弃权,每位同学只能推荐1人),每得1票记1分.
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按3:3:4的比例确定个人成绩,三人中谁会当选学生会主席?
 某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三明学生会干事中选拔一名干事当学生会主席,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按3:3:4的比例确定个人成绩,三人中谁会当选学生会主席?
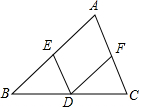 在△ABC中,点D、E、F分别是BC、AB、AC边的中点.求证:△BED≌△DFC.
在△ABC中,点D、E、F分别是BC、AB、AC边的中点.求证:△BED≌△DFC.
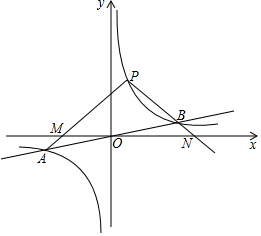 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.