题目内容
已知一个口袋中装有六个完全相同的小球,小球上分别标有0,3,6,9,12,15六个数,搅匀后一次从中摸出一个小球,将小球上的数记为a,则使得一次函数y=(5-a)x+a经过一、二、四象限且关于x的分式方程
=4+
的解为整数的概率是 .
| ax |
| x-6 |
| 6x |
| x-6 |
考点:概率公式,分式方程的解,一次函数图象与系数的关系
专题:
分析:由一个口袋中装有六个完全相同的小球,小球上分别标有0,3,6,9,12,15六个数,使得一次函数y=(5-a)x+a经过一、二、四象限且关于x的分式方程
=4+
的解为整数的有2种情况,直接利用概率公式求解即可求得答案.
| ax |
| x-6 |
| 6x |
| x-6 |
解答:解:∵一次函数y=(5-a)x+a经过一、二、四象限,
∴
,
解得:a>5,
∵关于x的分式方程
=4+
的解为整数,
则ax=4(x-6)+6x,
解得:x=-
,
∴a=9,12,
∴使得一次函数y=(5-a)x+a经过一、二、四象限且关于x的分式方程
=4+
的解为整数的有2种情况,
∴使得一次函数y=(5-a)x+a经过一、二、四象限且关于x的分式方程
=4+
的解为整数的概率是:
=
.
故答案为:
.
∴
|
解得:a>5,
∵关于x的分式方程
| ax |
| x-6 |
| 6x |
| x-6 |
则ax=4(x-6)+6x,
解得:x=-
| 24 |
| a-10 |
∴a=9,12,
∴使得一次函数y=(5-a)x+a经过一、二、四象限且关于x的分式方程
| ax |
| x-6 |
| 6x |
| x-6 |
∴使得一次函数y=(5-a)x+a经过一、二、四象限且关于x的分式方程
| ax |
| x-6 |
| 6x |
| x-6 |
| 2 |
| 6 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
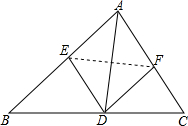 如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.
如图,在三角形纸片ABC中,AD平分∠BAC,将△ABC折叠,使点A与点D重合,展开后折痕分别交AB、AC于点E、F,连接DE、DF.求证:四边形AEDF是菱形.
 如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示
如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.