题目内容
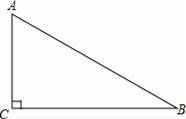
如图,在等边△ABC中,AD⊥BC于D,若AB=4cm,AD=2
 cm,E为AB的中点,P为AD上一点,PE+PB的最小值为 .
cm,E为AB的中点,P为AD上一点,PE+PB的最小值为 .


2
 .
.
【考点】轴对称-最短路线问题;等边三角形的性质.
【分析】连接EC交于AD于点P,由等腰三角形三线和一的性质可知AD是BC的垂直平分线,从而可证明BP=PC,故此PE+PB的最小值=EC,然后证明△ACE≌△CAD,从而得到EC=AD.
【解答】解:连接EC交于AD于点P.


∵AB=AC,BD=DC,
∴AD⊥BC.
∴AD是BC的垂直平分线.
∴PB=PC.
∴PE+PB=EP+PC=EC.
∵△ABC为等边三角形,
∴∠EAC=∠ACD=60°,AB=BC.
∵点E和点D分别是AB和BC的中点,
∴AE=DC.
在△ACE和△CAD中,
 ,
,
∴△ACE≌△CAD.
∴EC=AD=2
 .
.
故答案为:2
 .
.
【点评】本题主要考查的是轴对称路径最短问题,明确当点E、P、C在一条直线上时,PE+PB有最小值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 有意义,则x的取值是( )
有意义,则x的取值是( )