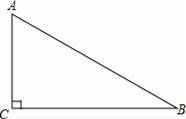
题目内容
如图,已知△ABC,∠C=90°,∠B=30°.
(1)用直尺和圆规在BC上找一点D,使DA=DB.(不写作法,保留作图痕迹)
(2)若BC=8,求点D到边AB的距离.

【考点】作图—复杂作图;线段垂直平分线的性质;含30度角的直角三角形.
【分析】(1)直接利用线段垂直平分线的作法得出答案;
(2)利用线段垂直平分线的性质得出∠DAB=∠B=30°,进而得出DC=DE,再得出2DE+DE=BC,求出答案即可.
【解答】解:(1)如图所示:点D即为所求;
(2)∵DE是AB的垂直平分线,
∴AD=DB,DE⊥AB,
∴∠DAB=∠B=30°,
∵∠BAC=60°,
∴∠CAD=∠DAB=30°,
∵∠C=90°,DE⊥AB,
∴DC=DE,
∵DE⊥AB,∠B=30°,
∴BD=2DE,
∴2DE+DE=BC=8,
∴DE=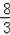
 .
.
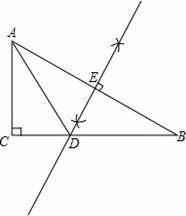

【点评】此题主要考查了复杂作图以及线段垂直平分线的性质与作法,正确掌握线段垂直平分线的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .如果点P由B出发沿BA向点A匀速运动,
.如果点P由B出发沿BA向点A匀速运动, ;
;


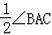
 ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC=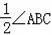


 cm,E为AB的中点,P为AD上一点,PE+PB的最小值为 .
cm,E为AB的中点,P为AD上一点,PE+PB的最小值为 .

 ( )
( )


 )÷
)÷
 ,再从﹣2≤a≤2中选一个你认为合适的整数作为a的值代入求值.
,再从﹣2≤a≤2中选一个你认为合适的整数作为a的值代入求值.