题目内容
18．已知一元二次方程x2-8x+16=0的两根分别是⊙O1和⊙O2的半径，若O1O2=6，则这两圆的位置关系是（ ）| A． | 内含 | B． | 相交 | C． | 外切 | D． | 外离 |
分析 首先解方程x2-8x+16=0，求得两圆半径r1、r2的值，又由两圆的圆心距为1，根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系，即可得出两圆位置关系．
解答 解：∵x2-8x+16=0，
∴x1x2=4，
即两圆半径r1、r2分别是4，3，
∵4-4＜6＜4+4，
∴两圆的位置关系是相交．
故选B．
点评 此题考查了圆与圆的位置关系与一元二次方程的解法．此题比较简单，注意掌握两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
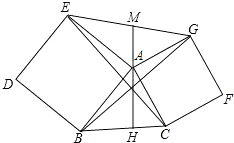如图，在锐角三角形ABC中，AH是BC边上的高，分别以AB、AC为一边，向外作正方形ABDE和ACEG，连接CE、BG和EG，EG与HA的延长线交于点M，下列结论：①BG=CE；②BG⊥CE；③AM是△AEG的中线；④∠EAM=∠ABC，其中正确的结论是①②③④．
13．使代数式$\sqrt{x+2}$-$\sqrt{1-2x}$有意义的x的取值范围是（ ）
| A． | x≥-2 | B． | x≤$\frac{1}{2}$ | C． | -2$≤x≤\frac{1}{2}$ | D． | 一切实数 |
如图，△ABC的角平分线BP、CP相交于点P，∠P=140°，求∠A的度数．