题目内容
因式分解
（1）n3（m-2）+n（2-m）．
（2）（x-a）（x-3a）+a2．
（1）n3（m-2）+n（2-m）．
（2）（x-a）（x-3a）+a2．
考点：提公因式法与公式法的综合运用
专题：计算题
分析：（1）原式提取公因式后，利用平方差公式分解即可；
（2）原式整理后，利用完全平方公式分解即可．
（2）原式整理后，利用完全平方公式分解即可．
解答：解：（1）原式=n（m-2）（n+1）（n-1）；
（2）原式=x2-4a+4a2
=（x-2a）2．
（2）原式=x2-4a+4a2
=（x-2a）2．
点评：此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
下列运算错误的是（ ）
A、(-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若单项式（a+2）x2ay3与
x4yb的和仍为单项式，则a，b的值分别是（ ）
| 1 |
| 2 |
| A、a=2，b=3 |
| B、a=-2，b=3 |
| C、a=2或-2，b=3 |
| D、a=0，b=3 |
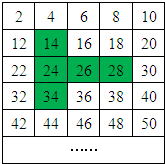如图，将连续的偶数2，4，6，8，10，…排成一数阵，有一个能够在数阵中上下左右平移的T字架，它可以框出数阵中的五个数．试判断这五个数的和能否为426？若能，请求出这五个数；若不能，请说明理由．