题目内容
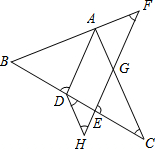 如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF 与AC相交于点G,∠BDA+∠CEG=180°.
如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF 与AC相交于点G,∠BDA+∠CEG=180°.(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,则∠F与∠H相等吗,请说明理由.
考点:平行线的判定与性质
专题:
分析:(1)求出∠ADE+∠FEB=180°,根据平行线的判定推出即可;
(2)根据角平分线定义得出∠BAD=∠CAD,推出HD∥AC,根据平行线的性质得出∠H=∠CGH,∠CAD=∠CGH,推出∠BAD=∠F即可.
(2)根据角平分线定义得出∠BAD=∠CAD,推出HD∥AC,根据平行线的性质得出∠H=∠CGH,∠CAD=∠CGH,推出∠BAD=∠F即可.
解答:解:(1)AD∥EF.
理由如下:∵∠BDA+∠CEG=180°,∠ADB+∠ADE=180°,∠FEB+∠CEF=180°
∴∠ADE+∠FEB=180°,
∴AD∥EF;
(2)∠F=∠H,
理由是:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠EDH=∠C,
∴HD∥AC,
∴∠H=∠CGH,
∵AD∥EF,
∴∠CAD=∠CGH,
∴∠BAD=∠F,
∴∠H=∠F.
理由如下:∵∠BDA+∠CEG=180°,∠ADB+∠ADE=180°,∠FEB+∠CEF=180°
∴∠ADE+∠FEB=180°,
∴AD∥EF;
(2)∠F=∠H,
理由是:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵∠EDH=∠C,
∴HD∥AC,
∴∠H=∠CGH,
∵AD∥EF,
∴∠CAD=∠CGH,
∴∠BAD=∠F,
∴∠H=∠F.
点评:本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,题目是一道比较好的题目,难度适中.

练习册系列答案
相关题目
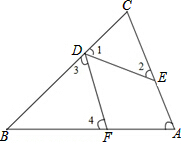 如图,在△ABC,∠A=70°,D、E、F分别在BC、AC、AB上,且∠1=∠2,∠3=∠4,则∠EDF等于( )
如图,在△ABC,∠A=70°,D、E、F分别在BC、AC、AB上,且∠1=∠2,∠3=∠4,则∠EDF等于( )| A、70° | B、65° |
| C、55° | D、45° |
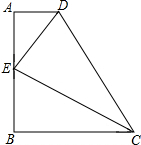 如图在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE.求证:
如图在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE.求证: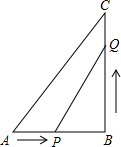 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始向B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P、Q分别从点A,B同时出发,经过多长时间△PBQ的面积等于6cm2?
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始向B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以3cm/s的速度移动,如果点P、Q分别从点A,B同时出发,经过多长时间△PBQ的面积等于6cm2? 如图,D、E分别是AB、AC的中点,CD⊥AB于D,BE⊥AC于E.
如图,D、E分别是AB、AC的中点,CD⊥AB于D,BE⊥AC于E.