题目内容
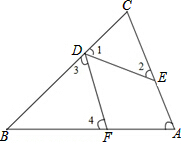 如图,在△ABC,∠A=70°,D、E、F分别在BC、AC、AB上,且∠1=∠2,∠3=∠4,则∠EDF等于( )
如图,在△ABC,∠A=70°,D、E、F分别在BC、AC、AB上,且∠1=∠2,∠3=∠4,则∠EDF等于( )| A、70° | B、65° |
| C、55° | D、45° |
考点:三角形内角和定理
专题:
分析:由已知可得∠1+∠3=180°-
(∠B+∠C),根据三角形的内角和定理求得∠B+∠C=180°-∠A=110°,然后根据平角的概念即可求得∠EDF的度数.
| 1 |
| 2 |
解答:解:∵∠1=∠2,∠3=∠4,
∴∠1=
(180°-∠C),∠3=
(180°-∠B),
∴∠1+∠3=180°-
(∠B+∠C),
∵∠B+∠C=180°-∠A=180°-70°=110°,
∴∠1+∠3=180°-
×110°=180°-55°,
∴∠EDF=180°-(∠1+∠3)=55°;
故选C.
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠3=180°-
| 1 |
| 2 |
∵∠B+∠C=180°-∠A=180°-70°=110°,
∴∠1+∠3=180°-
| 1 |
| 2 |
∴∠EDF=180°-(∠1+∠3)=55°;
故选C.
点评:本题考查了三角形的内角和定理,以及平角的概念,熟练掌握定理是关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
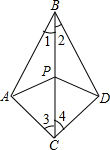 如图在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任意一点.求证:PA=PD.
如图在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任意一点.求证:PA=PD. 如图,△ABC中,AB=AC,DE⊥AB,垂足E为AB的中点,若AB+BC=26cm,则△BCD的周长是
如图,△ABC中,AB=AC,DE⊥AB,垂足E为AB的中点,若AB+BC=26cm,则△BCD的周长是 如图,在长为a、宽为b的长方形场地中,横向有两条宽均为n的长方形草坪,斜向有一条平行四边形的草坪,且其中一边长为m,则图中空地面积用含有a、b、m、n的代数式表示是
如图,在长为a、宽为b的长方形场地中,横向有两条宽均为n的长方形草坪,斜向有一条平行四边形的草坪,且其中一边长为m,则图中空地面积用含有a、b、m、n的代数式表示是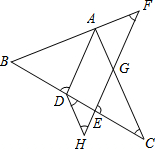 如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF 与AC相交于点G,∠BDA+∠CEG=180°.
如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF 与AC相交于点G,∠BDA+∠CEG=180°. 如图所示是某家庭去年开支的扇形统计图,根据统计图,回答下列问题:
如图所示是某家庭去年开支的扇形统计图,根据统计图,回答下列问题: