题目内容
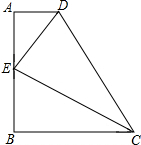 如图在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE.求证:
如图在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE.求证:(1)DE⊥EC;
(2)DE平分∠CDA;
(3)DC=AD+BC;
(4)S梯形ABCD=DE•EC.
考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:(1)作EF⊥CD于F,由角平分线的性质就可以得出BE=EF,得出AE=EF,△CEB≌△CEF,得出∠CEB=∠CEF,进而得出△AED≌△FED,就可以得出∠AED=∠FED,由∠AED+∠DEF+∠CEF+∠CEB=180°,就可以求出∠DEC=90°,进而得出结论;
(2)由△AED≌△FED就可以得出∠ADE=∠ADF,就可以得出结论;
(3)由△CEB≌△CEF就可以得出BC=FC,由△AED≌△FED就可以得出AD=FD,进而就可以得出结论;
(4)根据全等可以得出梯形ABCD的面积=2S△DEF+2S△CEF=2(S△DEF+S△CEF)=2S△DEC,由三角形的面积公式就可以得出结论.
(2)由△AED≌△FED就可以得出∠ADE=∠ADF,就可以得出结论;
(3)由△CEB≌△CEF就可以得出BC=FC,由△AED≌△FED就可以得出AD=FD,进而就可以得出结论;
(4)根据全等可以得出梯形ABCD的面积=2S△DEF+2S△CEF=2(S△DEF+S△CEF)=2S△DEC,由三角形的面积公式就可以得出结论.
解答:证明:(1)作EF⊥CD于F,
∴∠EFC=∠EFD=90°.
∵CE平分∠BCD,
∴∠BCE=∠FCE.
∵∠A=∠B=90°,
∴∠EFC=∠EFD=∠A=∠B=90°.
在△CEB和△CEF中,
,
∴△CEB≌△CEF(AAS),
∴BE=FE,BC=FC.∠CEB=∠CEF.
∵AE=BE,
∴AE=FE.
在Rt△AED和Rt△FED中,
,
∴Rt△AED≌Rt△FED(HL),
∴∠AED=∠FED,AD=FD.
∵∠CEB+∠CEF+∠AED+∠FED=180°,
∴2∠CEF+2∠DEF=180°,
∴∠CEF+∠DEF=90°,
即∠DEC=90°.
∴DE⊥CE;
(2)∵△AED≌△FED,
∴∠AED=∠FED,
∴DE平分∠CDA;
(3)∵BC=FC,AD=FD,
∴BC+AD=FC+FD,
∴DC=AD+BC
(4)∵△CEB≌△CEF,△AED≌△FED,
∴S△CEB=S△CEF,S△AED=S△FED.
∴S梯形ABCD=2S△DEF+2S△CEF=2(S△DEF+S△CEF)=2S△DEC.
∵S△DEC=
,
∴2S△DEC=DE•CE,
∴S梯形ABCD=DE•EC.
∴∠EFC=∠EFD=90°.
∵CE平分∠BCD,
∴∠BCE=∠FCE.
∵∠A=∠B=90°,
∴∠EFC=∠EFD=∠A=∠B=90°.
在△CEB和△CEF中,
|
∴△CEB≌△CEF(AAS),
∴BE=FE,BC=FC.∠CEB=∠CEF.
∵AE=BE,
∴AE=FE.
在Rt△AED和Rt△FED中,
|
∴Rt△AED≌Rt△FED(HL),
∴∠AED=∠FED,AD=FD.
∵∠CEB+∠CEF+∠AED+∠FED=180°,

∴2∠CEF+2∠DEF=180°,
∴∠CEF+∠DEF=90°,
即∠DEC=90°.
∴DE⊥CE;
(2)∵△AED≌△FED,
∴∠AED=∠FED,
∴DE平分∠CDA;
(3)∵BC=FC,AD=FD,
∴BC+AD=FC+FD,
∴DC=AD+BC
(4)∵△CEB≌△CEF,△AED≌△FED,
∴S△CEB=S△CEF,S△AED=S△FED.
∴S梯形ABCD=2S△DEF+2S△CEF=2(S△DEF+S△CEF)=2S△DEC.
∵S△DEC=
| DE•CE |
| 2 |
∴2S△DEC=DE•CE,
∴S梯形ABCD=DE•EC.
点评:本题考查了角平分线的性质的运用,平角的性质的运用,全等三角形的判定及性质的运用,三角形的面积公式的运用,梯形的面积公式的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,已知△ABC的面积是1,D、E、F和G、H、I分别是BC和AC边上的4等分点,则图中阴影部分的面积是( )
如图,已知△ABC的面积是1,D、E、F和G、H、I分别是BC和AC边上的4等分点,则图中阴影部分的面积是( )A、
| ||
B、
| ||
C、
| ||
D、
|

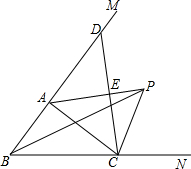 如图:△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
如图:△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.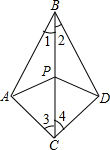 如图在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任意一点.求证:PA=PD.
如图在△ABC和△DBC中,∠1=∠2,∠3=∠4,P是BC上任意一点.求证:PA=PD. 为了提高市民的宜居环境,某区规划修建一个文化广场(平面图形如图所示),其中四边形ABCD是长方形,分别以AB、BC、CD、DA边为直径向外作半圆,若整个广场的周长为628米(π取3.14),BC边为97米.
为了提高市民的宜居环境,某区规划修建一个文化广场(平面图形如图所示),其中四边形ABCD是长方形,分别以AB、BC、CD、DA边为直径向外作半圆,若整个广场的周长为628米(π取3.14),BC边为97米.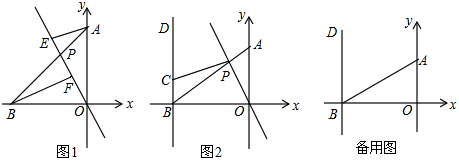
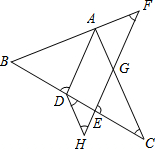 如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF 与AC相交于点G,∠BDA+∠CEG=180°.
如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF 与AC相交于点G,∠BDA+∠CEG=180°.