题目内容
10.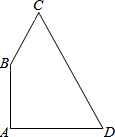 如图,在四边形ABCD中,∠A=90°,AB=9,AD=12,BC=8,CD=17.则四边形ABCD的面积是114.
如图,在四边形ABCD中,∠A=90°,AB=9,AD=12,BC=8,CD=17.则四边形ABCD的面积是114.
分析 连接BD,由勾股定理求出BD=15,求出BD2+BC2=CD2,由勾股定理的逆定理得出△BCD是直角三角形,∠CBD=90°,四边形ABCD的面积=△ABD的面积+CBD的面积,即可得出结果.
解答 解:连接BD,如图所示: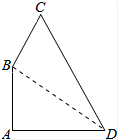
∵∠A=90°,AB=9,AD=12,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15,
∵BD2+BC2=152+82=189,CD2=172=189,
∴BD2+BC2=CD2,
∴△BCD是直角三角形,
∴∠CBD=90°,
∴四边形ABCD的面积=△ABD的面积+CBD的面积=$\frac{1}{2}$×9×12+$\frac{1}{2}$×15×8=54+60=114;
故答案为:114.
点评 本题考查了勾股定理、勾股定理的逆定理;熟练掌握勾股定理和勾股定理的逆定理,通过作辅助线证明三角形是直角三角形是解决问题的关键.

练习册系列答案
相关题目
1.sin30°的值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
5.下列方程中,一元二次方程是( )
| A. | ax2+bx+c=0 | B. | x+$\frac{1}{x}$=0 | C. | (x+1)(x-2)=3 | D. | x-2y=0 |
19. 如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )
如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )
 如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )
如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )| A. | a<b | B. | -a>b | C. | |a|<|b| | D. | -a>-b |
 如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP.
如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP.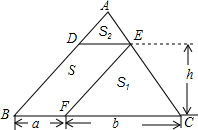 如图,在△ABC中,DE∥BC分别交AB、AC于D、E两点,过点E作EF∥AB交BC于点F.若BF=a,PC=b,DE与BC间的距离为h,求证:S2=4S1S2.
如图,在△ABC中,DE∥BC分别交AB、AC于D、E两点,过点E作EF∥AB交BC于点F.若BF=a,PC=b,DE与BC间的距离为h,求证:S2=4S1S2.