题目内容
20.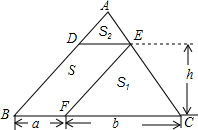 如图,在△ABC中,DE∥BC分别交AB、AC于D、E两点,过点E作EF∥AB交BC于点F.若BF=a,PC=b,DE与BC间的距离为h,求证:S2=4S1S2.
如图,在△ABC中,DE∥BC分别交AB、AC于D、E两点,过点E作EF∥AB交BC于点F.若BF=a,PC=b,DE与BC间的距离为h,求证:S2=4S1S2.
分析 由于DE∥BC,EF∥AB,可知四边形DBFE是?,同时,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,△EFC∽△ABC,从而易得△ADE∽△EFC,利用相似三角形的面积比等于相似比的平方,可得S1:S2=a2:b2,由于S1=$\frac{1}{2}$bh,那么可求S2,从而易求4S1S2,又S=ah,容易证出结论.
解答 证明:∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF,
∴△ADE∽△EFC,
∴$\frac{{S}_{2}}{{S}_{1}}$=($\frac{DE}{FC}$)2=$\frac{{a}^{2}}{{b}^{2}}$,
∵S1=$\frac{1}{2}$bh,
∴S2=$\frac{{a}^{2}}{{b}^{2}}$×S1=$\frac{{a}^{2}h}{2b}$,
∴4S1S2=4×$\frac{1}{2}$bh×$\frac{{a}^{2}h}{2b}$=(ah)2,
而S=ah,
∴S2=4S1S2.
点评 本题考查了平行四边形、三角形的面积公式,平行四边形的判定和性质、相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
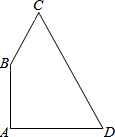 如图,在四边形ABCD中,∠A=90°,AB=9,AD=12,BC=8,CD=17.则四边形ABCD的面积是114.
如图,在四边形ABCD中,∠A=90°,AB=9,AD=12,BC=8,CD=17.则四边形ABCD的面积是114.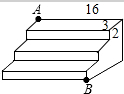 如图,是一个三级台阶,它的每一级的长、宽、高分别为16dm,3dm,2dm,A和B是这个台阶两相对的端点,A点有一只昆虫想到B点去吃可口的食物,则昆虫沿着台阶爬到B点最短路程是多少dm?
如图,是一个三级台阶,它的每一级的长、宽、高分别为16dm,3dm,2dm,A和B是这个台阶两相对的端点,A点有一只昆虫想到B点去吃可口的食物,则昆虫沿着台阶爬到B点最短路程是多少dm? 如图,求作一点P,使PA=PB,PC=PD(只保留作图痕迹,不要求写出作法)
如图,求作一点P,使PA=PB,PC=PD(只保留作图痕迹,不要求写出作法) 如图,已知牧马营地C和D,某一天,牧马人从营地C赶着马群,先带到草地吃草,再到河边饮水,然后回到营地D,请你替牧马人设计出最短路线.
如图,已知牧马营地C和D,某一天,牧马人从营地C赶着马群,先带到草地吃草,再到河边饮水,然后回到营地D,请你替牧马人设计出最短路线.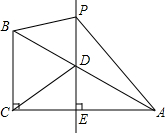 如图,在△ABC中,当∠ACB=90°,∠BAC=30°,BC=$\sqrt{3}$,过AB的中点D作DE⊥AC,垂足为点E,点P是直线DE上一动点,连结AP,BP,CD
如图,在△ABC中,当∠ACB=90°,∠BAC=30°,BC=$\sqrt{3}$,过AB的中点D作DE⊥AC,垂足为点E,点P是直线DE上一动点,连结AP,BP,CD
