题目内容
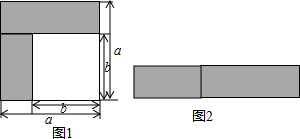
 根据如图所给信息,回答下列问题:
根据如图所给信息,回答下列问题:(1)分别求出桌子和椅子的单价是多少?
(2)学校根据实际情况,要求购买桌椅总费用不超过1000元,并且购买桌子的数量是椅子数量的
| 5 |
| 2 |
(3)厂家为了搞促销活动,推出凡一次性购买桌子和椅子的数量共28张以上(含28张),可享受八折优惠,请问该校在满足(2)的条件下,最多能购买多少张桌子?多少张椅子?总费用是多少元?
考点:一元一次不等式组的应用,二元一次方程组的应用,一元一次不等式的应用
专题:
分析:(1)设每张椅子x元,每张桌子y元.由桌子和椅子的单价与总价的关系建立二元一次方程组求出其解即可;
(2)设学校购买a张椅子,则桌子的数量为
a张.根据购买桌椅总费用不超过1000元建立不等式组,求出其解即可;
(3)设学校最多能购买m张椅子,则桌子的数量为
m张,由条件建立不等式组求出其解即可.
(2)设学校购买a张椅子,则桌子的数量为
| 5 |
| 2 |
(3)设学校最多能购买m张椅子,则桌子的数量为
| 5 |
| 2 |
解答:解:(1)设每张椅子x元,每张桌子y元.根据题意,得
,
解得:
.
答:每张椅子20元,每张桌子50元;
(2)设学校购买a张椅子,则桌子的数量为
a张.根据题意,得
20a+50×
a≤1000,
解得:a≤
…3′
∵a,
a均为正整数.
∴a=6或4或2.
∴学校购买桌椅共3种方案.
第一种方案:购买6张椅子、15张桌子.
第二种方案:购买4张椅子、10张桌子.
第三种方案:购买2张椅子、5张桌子.
(3)设学校最多能购买m张椅子,则桌子的数量为
m张,根据题意,得
,
解得:8≤m≤
,
∵m、
m的取值均要为正整数,
∴m=8.
即:学校最多能购买8张椅子、20张桌子.
(20×8+50×20)×0.8=928(元).
答:学校最多购买8张椅子、20张桌子,总费用为928元.
|
解得:
|
答:每张椅子20元,每张桌子50元;
(2)设学校购买a张椅子,则桌子的数量为
| 5 |
| 2 |
20a+50×
| 5 |
| 2 |
解得:a≤
| 200 |
| 29 |
∵a,
| 5 |
| 2 |
∴a=6或4或2.
∴学校购买桌椅共3种方案.
第一种方案:购买6张椅子、15张桌子.
第二种方案:购买4张椅子、10张桌子.
第三种方案:购买2张椅子、5张桌子.
(3)设学校最多能购买m张椅子,则桌子的数量为
| 5 |
| 2 |
|
解得:8≤m≤
| 250 |
| 29 |
∵m、
| 5 |
| 2 |
∴m=8.
即:学校最多能购买8张椅子、20张桌子.
(20×8+50×20)×0.8=928(元).
答:学校最多购买8张椅子、20张桌子,总费用为928元.
点评:本题考查了列二元一次方程组解实际问题的运用,列一元一次不等式组及不等式解实际问题的运用,设计方案的运用,解答时根据条件建立方程及不等式是关键.

练习册系列答案
相关题目
 已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.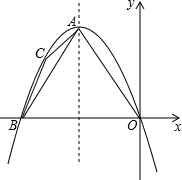 如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=-2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为
如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=-2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为 如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是
如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是