题目内容
“三月三上孤山”,孤山某商店决定购进A、B两种纪念品.若购进A种纪念品8件,B种纪念品4件,需要1000元;若购进A种纪念品5件,B种纪念品7件,需要850元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润40元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,若全部销售结束后,哪一种方案获利最大?最大利润是多少元?
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润40元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,若全部销售结束后,哪一种方案获利最大?最大利润是多少元?
考点:一元一次不等式组的应用,二元一次方程组的应用
专题:
分析:(1)设该商场购进一件A中纪念品需要x元,购进一件B种纪念品需要y元,根据购买商品的数量级价格之间的关系建立方程组求出其解即可;
(2)设该商店购进A种纪念品a件,则购进B种纪念品(100-a)套,根据条件中的不相等关系建立不等式组求出其解即可;
(3)设总利润为W元,根据总利润=A种纪念品的利润+B种纪念品的利润就可以表示出W与x的关系式,由一次函数的性质求出其解即可.
(2)设该商店购进A种纪念品a件,则购进B种纪念品(100-a)套,根据条件中的不相等关系建立不等式组求出其解即可;
(3)设总利润为W元,根据总利润=A种纪念品的利润+B种纪念品的利润就可以表示出W与x的关系式,由一次函数的性质求出其解即可.
解答:解:(1)设该商场购进一件A中纪念品需要x元,购进一件B种纪念品需要y元,由题意,得
,
解得:
.
答:该商场购进一件A中纪念品需要100元,购进一件B种纪念品需要50元;
(2)设该商店购进A种纪念品a件,则购进B种纪念品(100-a)套,由题意,得
,
解得:50≤a≤53.
∵a为整数,
∴a=50,51,52,53.
∴共有4种进货方案;
(3)设总利润为W元,由题意,得
W=40a+30(100-a),
=10a+3000.
∴k=10>0,
∴W随x的增大而增大,
∴W最大=10×53+3000=3530元.
|
解得:
|
答:该商场购进一件A中纪念品需要100元,购进一件B种纪念品需要50元;
(2)设该商店购进A种纪念品a件,则购进B种纪念品(100-a)套,由题意,得
|
解得:50≤a≤53.
∵a为整数,
∴a=50,51,52,53.
∴共有4种进货方案;
(3)设总利润为W元,由题意,得
W=40a+30(100-a),
=10a+3000.
∴k=10>0,
∴W随x的增大而增大,
∴W最大=10×53+3000=3530元.
点评:本题考查了列二元一次方程组解实际问题的运用,列一元一次不等式组解实际问题的运用,一次函数的解析式的运用,解答时由销售问题的数量关系建立方程或不等式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中,点P(-3,4)关于y轴对称点的坐标为( )
| A、(-3,4) |
| B、(3,4) |
| C、(3,-4) |
| D、(-3,-4) |
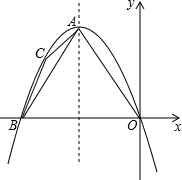 如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=-2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为
如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=-2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为