题目内容
已知x3+x2+x+1=0，求1+x+x2+x3+x4+x5+…+x2007的值．
考点：因式分解的应用
专题：
分析：把1+x+x2+x3+x4+x5+…+x2007化为（1+x+x2+x3）+x4（1+x+x2+x3）…+x2003（1+x+x2+x3）求解即可．
解答：解：1+x+x2+x3+x4+x5+…+x2007=（1+x+x2+x3）+x4（1+x+x2+x3）…+x2003（1+x+x2+x3）
∵x3+x2+x+1=0，
∴原式=0．
∵x3+x2+x+1=0，
∴原式=0．
点评：本题主要考查了因式分解的应用，解题的关键是从式子中找出关于x3+x2+x+1的式子．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
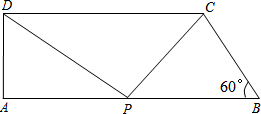如图，在直角梯形ABCD中，AB∥CD，AD⊥AB，∠B=60°，AB=10，BC=4，点P沿线段AB从点A向点B运动，设AP=x．