题目内容
10.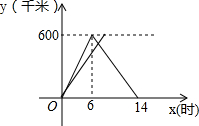 A、B两地相距600千米,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即返回,它们各自离A地的距离y(千米)与行驶时间x(时)之间的函数关系图象如图所示.
A、B两地相距600千米,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即返回,它们各自离A地的距离y(千米)与行驶时间x(时)之间的函数关系图象如图所示.(1)求甲车行驶过程中y与x之间的函数关系式;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度.
分析 (1)根据函数图象可以得到甲车行驶过程中y与x之间的函数关系式;
(2)根据(1)求得函数解析式,可以得到当x=7时的y值,然后用求得的y值除以7即可求得乙车的速度.
解答 解:(1)当0≤x≤6时,设甲车行驶过程中y与x之间的函数关系式为y=mx,
把(6,600)代入y=mx,
6m=600,
解得m=100,
∴y=100x;
当6<x≤14时,设甲车行驶过程中y与x之间的函数关系式为y=kx+b,
把(6,600)、(14,0)代入y=kx+b,
得$\left\{\begin{array}{l}{6k+b=600}\\{14k+b=0}\end{array}\right.$
解得,$\left\{\begin{array}{l}{k=-75}\\{b=1050}\end{array}\right.$
∴y=-75x+1 050;
即甲车行驶过程中y与x之间的函数关系式为:y=$\left\{\begin{array}{l}{100x}&{0≤x≤6}\\{-75x+1050}&{6<x≤14}\end{array}\right.$;
(2)当x=7时,y=-75x+1 050
解得,y=-75×7+1 050=525,
525÷7=75(千米/时),
即乙车的速度为75千米/时.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
1.已知$\sqrt{x+3}$+|y-2|=0,那么x+y的值是( )
| A. | 1 | B. | -1 | C. | -3 | D. | 2 |
 小芳从正面(图示“主视方向”)观察如图的热水瓶时,得到的主视图是( )
小芳从正面(图示“主视方向”)观察如图的热水瓶时,得到的主视图是( )




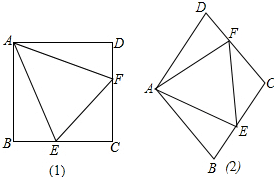 (1)如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
(1)如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.