题目内容
6.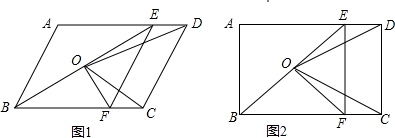 如图1,已知在四边形ABCD中,AD∥BC,AB∥CD,BE平分∠ABC,交AD于点E,过点E作EF∥AB,交BC于点F,O是BE的中点,连接OF,OC,OD.
如图1,已知在四边形ABCD中,AD∥BC,AB∥CD,BE平分∠ABC,交AD于点E,过点E作EF∥AB,交BC于点F,O是BE的中点,连接OF,OC,OD.(1)求证:四边形ABFE是菱形;
(2)若∠ABC=90°,如图2所示:
①求证:∠ADO=∠BCO;
②若∠EOD=15°,求∠OCD的度数.
分析 (1)根据平行四边形的性质得出AD∥BC,求出四边形ABFE是平行四边形,求出AB=AE,根据菱形的判定得出即可;
(2)①过O作ON∥BC交DC于N,根据矩形的判定得出四边形ABCD是矩形,根据矩形的性质得出∠ADC=∠BCD=90°,AD∥BC,求出N为DC的中点,ON⊥DC,根据线段垂直平分线性质得出OD=OC,即可得出答案;
②根据正方形的判定得出四边形ABFE是正方形,根据正方形的性质得出∠AEB=45°,根据三角形外角性质求出∠ADO=30°,求出∠ODC即可.
解答 证明:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AE∥BF,
∵EF∥AB,
∴四边形ABFE是平行四边形,
∵AE∥BF,
∴∠AEB=∠ABE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∴平行四边形ABFE是菱形;
(2)①过O作ON∥BC交DC于N,
∵AD∥BC,AB∥CD,∠ABC=90°,
∴四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,AD∥BC,
∴AD∥ON∥BC,
∵O为BE的中点,
∴N为DC的中点,ON⊥DC,
∴OD=OC,
∴∠ODC=∠OCD,
∵∠ADC=∠BCD=90°,
∴∠ADO=∠BCO;
②解:∵四边形ABFE是平行四边形,AB=AE,∠ABC=90°,
∴四边形ABFE是正方形,
∴∠AEB=$\frac{1}{2}$∠AEF=$\frac{1}{2}$×90°=45°,
∵∠EOD=15°,
∴∠EDO=∠AEB-∠EOD=45°-15°=30°,
∴∠ODC=∠ADC-∠EDO=90°-30°=60°,
∵∠OCD=∠ODC,
∴∠OCD=60°.
点评 本题考查了矩形的性质和判定,菱形的性质和判定,正方形的性质和判定,等腰三角形的性质和判定,平行四边形的性质和判定的应用,能综合运用定理进行推理是解此题的关键.

| A. | a-2<b-2 | B. | -2a<-2b | C. | |a|>|b| | D. | a2>b2 |
| A. | -6 | B. | 6 | C. | -3 | D. | 3 |
| A. | m<1 | B. | m>-2 | C. | m<-2 | D. | -2<m<1 |
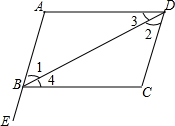 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠C=∠CBE | D. | ∠C+∠ABC=180° |
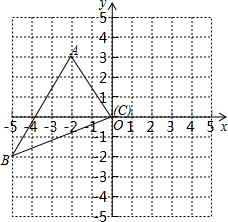 △ABC的位置如图所示:
△ABC的位置如图所示: