题目内容
13.等腰三角形的底角为15°,腰长为a,则此三角形的面积为$\frac{1}{4}$a2.分析 作一腰上的高,利用30°所对的直角边等于斜边的一半,得到腰上的高为$\frac{1}{2}$a,运用三角形的面积公式解答.
解答 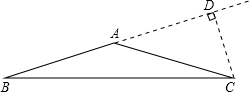 解:如图所示,在三角形ABC中,AB=AC=a,∠B=∠ACB=15°.
解:如图所示,在三角形ABC中,AB=AC=a,∠B=∠ACB=15°.
作CD⊥BA于点D,
则∠CAD=∠B+∠ACB=30°.
在Rt△ADC中,CD=$\frac{1}{2}$AC=$\frac{1}{2}$a,
S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$a•$\frac{1}{2}$a=$\frac{1}{4}$a2.
故答案为$\frac{1}{4}$a2.
点评 此题考查了含30°角的直角三角形的性质,三角形的外角性质,以及等腰三角形的性质,解题的关键是作出相应的辅助线CD,灵活运用各种性质来解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
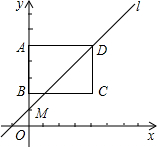 如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)、(0,2)、(4,2),直线l的解析式为y=kx+5-4k(k>0).
如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)、(0,2)、(4,2),直线l的解析式为y=kx+5-4k(k>0).