题目内容
观察下面一列数,探究其中的规律:-1, ,
, ,
, ,
,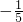 ,
,
①填空:第7、8个数分别是________,________;
②第2012个数是________.
-


分析:(1)把1等价于 ,经观察发现每一项的分子分别是1,分母等于各自的序号,如分母分别是1,2,3,4,5,6…又知奇数项是负数,偶数项是正数,所以第7,8个数是-
,经观察发现每一项的分子分别是1,分母等于各自的序号,如分母分别是1,2,3,4,5,6…又知奇数项是负数,偶数项是正数,所以第7,8个数是- ,
, ,
,
(2)根据(1)中所求得出第2012个数的值.
解答:(1)将-1等价于- ,即:-
,即:- ,
, ,
, ,
, ,
,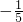 ,
, ,
,
可以发现分子永远为1,分母等于序数,奇数项为负数,偶数项为正,由此可以推出第n个数是(-1)n ,
,
所以第7个数是(-1)7 =-
=- ,第8个数是(-1)8×
,第8个数是(-1)8× =
= ,
,
(2)第2012个数为:(-1)2012× =
= .
.
故答案为:- ,
, ;
; .
.
点评:此题主要考查了数字变化规律,由题中所给的一列数推出第n个数为(-1)n 的规律是解题关键.
的规律是解题关键.



分析:(1)把1等价于
 ,经观察发现每一项的分子分别是1,分母等于各自的序号,如分母分别是1,2,3,4,5,6…又知奇数项是负数,偶数项是正数,所以第7,8个数是-
,经观察发现每一项的分子分别是1,分母等于各自的序号,如分母分别是1,2,3,4,5,6…又知奇数项是负数,偶数项是正数,所以第7,8个数是- ,
, ,
,(2)根据(1)中所求得出第2012个数的值.
解答:(1)将-1等价于-
 ,即:-
,即:- ,
, ,
, ,
, ,
,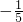 ,
, ,
,可以发现分子永远为1,分母等于序数,奇数项为负数,偶数项为正,由此可以推出第n个数是(-1)n
 ,
,所以第7个数是(-1)7
 =-
=- ,第8个数是(-1)8×
,第8个数是(-1)8× =
= ,
,(2)第2012个数为:(-1)2012×
 =
= .
.故答案为:-
 ,
, ;
; .
.点评:此题主要考查了数字变化规律,由题中所给的一列数推出第n个数为(-1)n
 的规律是解题关键.
的规律是解题关键. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目