题目内容
 如图,已知AD是△ABC的角平分线,过B作BF垂直AD交AD的延长线于点E,交AC的延长线于点F,试说明∠α+∠β=2∠F的理由.
如图,已知AD是△ABC的角平分线,过B作BF垂直AD交AD的延长线于点E,交AC的延长线于点F,试说明∠α+∠β=2∠F的理由.考点:三角形的外角性质,三角形内角和定理
专题:
分析:由BF垂直AD及AD是△ABC的角平分线,可得∠ABE=∠F,然后由外角的性质可得β=∠1+∠F,进而得到:α+β=α+∠1+∠F而α+∠1=∠ABE,进而可得α+β=∠ABE+∠F,从而可得α+β=2∠F.
解答:解:如图所示,

∵BF垂直AD,
∴∠AEB=∠AEF=90°,
∵AD是△ABC的角平分线,
∴∠2=∠3,
∵∠2+∠ABE+∠AEB=180°,
∠3+∠F+∠AEF=180°,
∴∠ABE=∠F,
∵β是△BCF的外角,
∴β=∠1+∠F,
∴α+β=α+∠1+∠F,
∵α+∠1=∠ABE,
∴α+β=∠ABE+∠F,
即α+β=2∠F.

∵BF垂直AD,
∴∠AEB=∠AEF=90°,
∵AD是△ABC的角平分线,
∴∠2=∠3,
∵∠2+∠ABE+∠AEB=180°,
∠3+∠F+∠AEF=180°,
∴∠ABE=∠F,
∵β是△BCF的外角,
∴β=∠1+∠F,
∴α+β=α+∠1+∠F,
∵α+∠1=∠ABE,
∴α+β=∠ABE+∠F,
即α+β=2∠F.
点评:此题考查了三角形外角的性质,解题的关键是:熟记三角形外角的性质,三角形的外角等于与它不相邻的两个内角之和.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米(小方格的边长为1厘米)
蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米(小方格的边长为1厘米)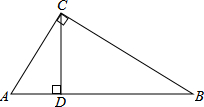 如图,在Rt△ABC中,∠C=90°,BC=15,AB-AC=9,CD⊥AB于点D,求CD的长.
如图,在Rt△ABC中,∠C=90°,BC=15,AB-AC=9,CD⊥AB于点D,求CD的长.