题目内容
8．
如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，垂足为D，已知CD=4，OD=3，求AB的长．
分析 连接OC，根据勾股定理求出OC的长，进而可得出结论．
解答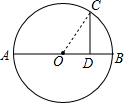 
解：连接OC，
∵CD⊥AB，垂足为D，CD=4，OD=3，
∴OC=$\sqrt{{OD}^{2}+{CD}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴AB=2OC=10．
点评 本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
实数a，b在数轴上的位置如图所示，化简$\sqrt{（b-a）^{2}}$+|a+b|-$\sqrt{{a}^{2}}$．
正方形ABCD，E、F分别为BC、CD边上一点，AH⊥EF交EF于点H．
13．下列格式中，无意义的是（ ）
| A． | $\sqrt{-{3}^{2}}$ | B． | $\root{3}{（-3）^{3}}$ | C． | $\sqrt{（-3）^{2}}$ | D． | $\sqrt{-3+4}$ |
如图，已知线段AB=10，点C是直线AB上方一个动点，∠ACB=m°，
17．下列各图中表示数轴的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
18．$\frac{3}{8}$的绝对值和相反数分别是（ ）
| A． | $-\frac{3}{8}$，$-\frac{3}{8}$ | B． | $\frac{3}{8}$，$\frac{3}{8}$ | C． | $-\frac{3}{8}$，$\frac{3}{8}$ | D． | $\frac{3}{8}$，$-\frac{3}{8}$ |