题目内容
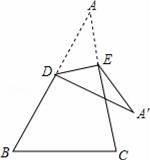
如图,在△ABC中,沿DE折叠,点A落在三角形所在的平面内的点为A1,若∠A=30°,∠BDA1=80°,则∠CEA1的度数为 .

20°【考点】翻折变换(折叠问题).
【分析】由∠BDA1=80°,可知邻补角的度数,根据折叠的性质知∠ADE=∠A1DE,又∠A=30°,运用三角形的外角和求出∠DEC=80°,再根据邻补角定义和折叠的性质知∠AED=∠A1ED=100°,从而∠CEA1=∠A1ED﹣∠DEC=20°.
【解答】解:∵∠BDA1=80°,
∴∠ADA1=100°,
根据折叠的性质知∠ADE=∠A1DE=
 ,∠ADA1=50°,
,∠ADA1=50°,
又∵∠A=30°,
∴∠DEC=80°,
∴∠AED=∠A1ED=100°,
∴∠CEA1=∠A1ED﹣∠DEC=20°.
故答案为:20°.
【点评】本题考查了翻折变换(折叠问题)、三角形内角和及角的和差,熟悉折叠的性质是解决问题的关键.折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
 ,
, (其中
(其中 表示数的个
表示数的个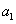 表示第一个数,
表示第一个数,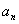 表示最后一个数).所以,
表示最后一个数).所以,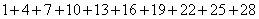 =
=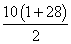
 .
.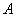 、
、 分别拟定上缴利润方案
分别拟定上缴利润方案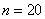 时,通过计算说明哪个企业上缴利润的总金额比较多?多多少万元?
时,通过计算说明哪个企业上缴利润的总金额比较多?多多少万元?