题目内容
10. 如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( )
如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( )| A. | $\frac{1}{{{2^{2013}}}}$ | B. | $\frac{1}{{{2^{2014}}}}$ | C. | $\frac{1}{{{2^{2015}}}}$ | D. | $\frac{1}{{{2^{2016}}}}$ |
分析 根据矩形的对角线互相平分,平行四边形的对角线互相平分可得下一个图形的面积是上一个图形的面积的$\frac{1}{2}$,然后求解即可.
解答 解:∵O1为矩形ABCD的对角线的交点,
∴平行四边形AOC1B底边AB上的高等于BC的$\frac{1}{2}$,
∴平行四边形AOC1B的面积=$\frac{1}{2}$×1=$\frac{1}{2}$,
∵平行四边形AO1C2B的对角线交于点O2,
∴平行四边形AOC2B的边AB上的高等于平行四边形AOC1B底边AB上的高的$\frac{1}{2}$,
∴平行四边形ABC3O2的面积=$\frac{1}{2}$×$\frac{1}{2}$×1=$\frac{1}{{2}^{2}}$,
…,
依此类推,平行四边形ABC2014O2015的面积=$\frac{1}{{2}^{2015}}$cm2.
故选:C.
点评 此题主要考查了学生矩形和平行四边形的有关知识,要求考生具备有从特殊到一般的数学思考方法和有较强的归纳探究能力,才能正确地作出解答.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
1.已知x-y≠0,且2x-3y=0,则分式$\frac{2x-y}{x-y}$的值为( )
| A. | -6 | B. | -1 | C. | 2 | D. | 4 |
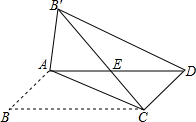 如图,在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′C,B′D,B′C交AD于点E.
如图,在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′C,B′D,B′C交AD于点E.