题目内容
16.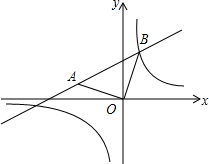 如图,在平面直角坐标系中,A(-3,1),以点O为顶点作等腰直角三角形AOB,双曲线y1=$\frac{{k}_{1}}{x}$在第一象限内的图象经过点B.设直线AB的解析式为y2=k2x+b,当y1>y2时,x的取值范围是( )
如图,在平面直角坐标系中,A(-3,1),以点O为顶点作等腰直角三角形AOB,双曲线y1=$\frac{{k}_{1}}{x}$在第一象限内的图象经过点B.设直线AB的解析式为y2=k2x+b,当y1>y2时,x的取值范围是( )| A. | -5<x<1 | B. | 0<x<1或x<-5 | C. | -6<x<1 | D. | 0<x<1或x<-6 |
分析 由△AOB是等腰三角形,先求的点B的坐标,然后利用待定系数法可求得双曲线和直线的解析式,然后将将y1=$\frac{3}{x}$与y2=$\frac{1}{2}x+\frac{5}{2}$联立,求得双曲线和直线的交点的横坐标,然后根据图象即可确定出x的取值范围.
解答 解:如图所示: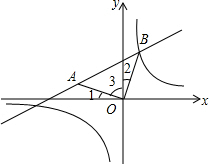
∵△AOB为等腰直角三角形,
∴OA=OB,∠3+∠2=90°.
又∵∠1+∠3=90°,
∴∠1=∠2.
∵点A的坐标为(-3,1),
∴点B的坐标(1,3).
将B(1,3)代入反比例函数的解析式得:3=$\frac{k}{1}$,
∴k=3.
∴y1=$\frac{3}{x}$
将A(-3,1),B(1,3)代入直线AB的解析式得:$\left\{\begin{array}{l}{-3{k}_{2}+b=1}\\{{k}_{2}+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=\frac{1}{2}}\\{b=\frac{5}{2}}\end{array}\right.$,
∴直线AB的解析式为y2=$\frac{1}{2}x+\frac{5}{2}$.
将y1=$\frac{3}{x}$与y2=$\frac{1}{2}x+\frac{5}{2}$联立得;$\left\{\begin{array}{l}{{y}_{2}=\frac{1}{2}x+\frac{5}{2}}\\{{y}_{1}=\frac{3}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{x}_{2}=-6}\end{array}\right.$,
当y1>y2时,双曲线位于直线线的上方,
∴x的取值范围是:x<-6或0<x<1.
故选:D.
点评 本题主要考查了反比例函数和一次函数的交点问题,求得双曲线和直线的交点的横坐标是解题的关键,同时本题还考查了函数与不等式的关系:从函数的角度看,y1>y2就是双曲线y1=$\frac{3}{x}$位于直线y2=$\frac{1}{2}x+\frac{5}{2}$上方部分所有点的横坐标的集合;从不等式的角度来看y1>y2就是求不等式$\frac{3}{x}$>$\frac{1}{2}x+\frac{5}{2}$的解集.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案| A. | 了解某班学生对中国首辆月球车--“玉兔”的知晓情况 | |
| B. | 了解某市中学生每天体育锻炼的时间 | |
| C. | 了解某市市民对城市建设的满意度 | |
| D. | 了解南方人对雾霾危害的了解情况 |
 如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=60°.
如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=60°.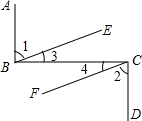 已知:如图AB⊥BC,BC⊥CD且∠1=∠2,试说明:BE∥CF.
已知:如图AB⊥BC,BC⊥CD且∠1=∠2,试说明:BE∥CF. 某宾馆铺地毯,已知主楼梯宽3米,其余数据如图所示,需购地毯多少平方米?
某宾馆铺地毯,已知主楼梯宽3米,其余数据如图所示,需购地毯多少平方米? 如图,数轴上标出若干个点,每个相邻两点距离相等,点A,B,C,D对应的数分别是数a,b,c,d,a+b+c+d=2,a-b+c-d=-3,求a点位置.
如图,数轴上标出若干个点,每个相邻两点距离相等,点A,B,C,D对应的数分别是数a,b,c,d,a+b+c+d=2,a-b+c-d=-3,求a点位置.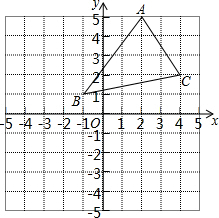 如图,将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A′B′C′,且点A,B,C的对应点分别为点A′,B′,C′.
如图,将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A′B′C′,且点A,B,C的对应点分别为点A′,B′,C′.