题目内容
13.已知AB为⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于点E,∠CAB=30°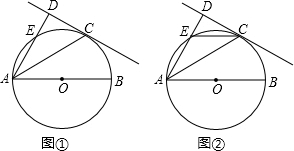
(1)如图①,求∠DAC的大小;
(2)如图②,若⊙O的半径为4,求DE的长.
分析 (1)连接OC,如图①,根据切线的性质得OC⊥DC,而AD⊥DC,则可判断AD∥OC,根据平行线的性质得∠DAC=∠ACO,加上∠OCA=∠CAB=30°,所以∠DAC=30°,
(2)连OE,OC,如图②,根据圆周角定理得到∠EOC=2∠DAC=60°,于是可判断△OEC为等边三角形,则EC=OE=4,∠OCE=60°,所以∠DCE=30°,于是根据含30度的直角三角形三边的关系可得DE=$\frac{1}{2}$CE=2.
解答 解:(1)连接OC,如图①,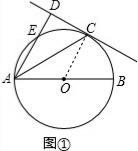
∵DC切⊙O于点C,
∴OC⊥DC,
又∵AD⊥DC,
∴AD∥OC
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OCA=∠CAB=30°,
∴∠DAC=30°;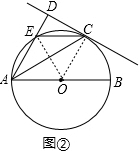
(2)连OE,OC,如图②,
∵∠EOC=2∠DAC=60°,
∴△OEC为等边三角形,
∴EC=OE=4,∠OCE=60°,
∴∠DCE=30°,
∴DE=$\frac{1}{2}$CE=2.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
1.某学习小组7位同学,为地震灾区捐款,捐款金额分别为5元、6元、6元、6元、7元、8元、9元,则这组数据的中位数与众数分别为( )
| A. | 6,6 | B. | 7,6 | C. | 7,8 | D. | 6,8 |
8.长沙地铁2号线于2013年12月30日试通车,规划总长约210000米,用科学记数法表示这个总长为( )
| A. | 2.1×105米 | B. | 2.1×106米 | C. | 0.21×106米 | D. | 21×104米 |
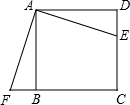 已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.