题目内容
13.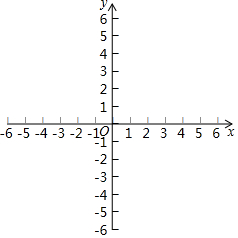 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-2,0),B(0,-2$\sqrt{3}$),C(4,0),其中对称轴与x轴交于点D.
如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-2,0),B(0,-2$\sqrt{3}$),C(4,0),其中对称轴与x轴交于点D.(1)求二次函数的表达式及其顶点坐标;
(2)点M在抛物线的对称轴上,若△ABM为等腰三角形,则符合题意的点M有5个;
(3)点P是直线x=2上的一个动点,若∠APB不小于60°,求点P的纵坐标P的取值范围.
分析 (1)根据抛物线经过A(-2,0),C(4,0)设抛物线的解析式为y=a(x+2)(x-4),把B(0,-2$\sqrt{3}$)代入得a=$\frac{\sqrt{3}}{4}$,由此即可解决问题.
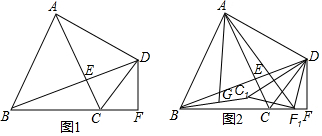
(2)如图1中,当AM=AB时,对称轴时有两个点满足条件M1与M2,当BM=BA时,对称轴上也有两个点满足条件M3,M4,大部分MA=MB时,只有一个点满足条件M5.所以满足条件的点有5个,
(3)由tan∠OAB=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,推出∠OAB=60°,∠ABO=30°,推出AB=2OA=4,设直线x=2与x轴交于点G(2,0),则△ABG是等边三角形,作△ABG的外接圆交直线x=2于K点,由∠AKB=∠AG′B=60°,推出当点P在线段GK上时,∠APB不小于60°,求出点K的坐标即可解决问题.
解答 解:(1)∵抛物线经过A(-2,0),C(4,0)
∴设抛物线的解析式为y=a(x+2)(x-4),把B(0,-2$\sqrt{3}$)代入得a=$\frac{\sqrt{3}}{4}$,
∴抛物线的解析式为y=$\frac{\sqrt{3}}{4}$(x+2)(x-4),即y=$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{2}$x-2$\sqrt{3}$.
∵y=$\frac{\sqrt{3}}{4}$x2-$\frac{\sqrt{3}}{2}$x-2$\sqrt{3}$=$\frac{\sqrt{3}}{4}$(x-1)2-$\frac{9\sqrt{3}}{4}$,
∴顶点坐标为(1,-$\frac{9\sqrt{3}}{4}$).
(2)如图1中,当AM=AB时,对称轴时有两个点满足条件M1与M2,当BM=BA时,对称轴上也有两个点满足条件M3,M4,大部分MA=MB时,只有一个点满足条件M5.所以满足条件的点有5个,
故答案为5.
(3)如图2中,
∵tan∠OAB=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠OAB=60°,∠ABO=30°,
∴AB=2OA=4,设直线x=2与x轴交于点G(2,0),则△ABG是等边三角形,作△ABG的外接圆交直线x=2于K点,
∵∠AKB=∠AG′B=60°,
∴当点P在线段GK上时,∠APB不小于60°,
易知△ABG的外接圆的圆心坐标为(0,-$\frac{2\sqrt{3}}{3}$),设K(2,m),
则有$\frac{4\sqrt{3}}{3}$=$\sqrt{{2}^{2}+(m+\frac{2\sqrt{3}}{3})^{2}}$,
解得:m=0或-$\frac{4\sqrt{3}}{3}$,
∴满足条件的点P的纵坐标P的取值范围-$\frac{4\sqrt{3}}{3}$≤m≤0.
点评 本题考查二次函数综合题、等腰三角形的判定和性质、等边三角形的判定和性质,三角形的外接圆的有关性质等知识,解题的关键是学会用分类讨论的思考思考问题,学会添加常用辅助线(构造辅助圆)解决问题,属于中考压轴题.

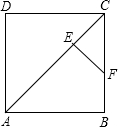 已知:如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交BC于F.求证:BF=EC.
已知:如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交BC于F.求证:BF=EC.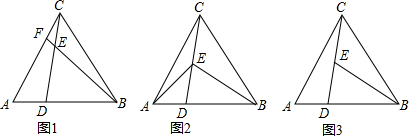
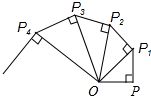 如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.
如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.



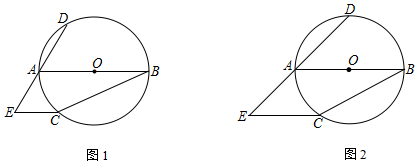
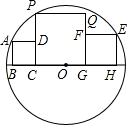 如图,3个正方形在⊙O直径的同侧,顶点B,C,G,H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上,顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则正方形PCGQ的面积为( )
如图,3个正方形在⊙O直径的同侧,顶点B,C,G,H都在⊙O的直径上,正方形ABCD的顶点A在⊙O上,顶点D在PC上,正方形EFGH的顶点E在⊙O上,顶点F在QG上,正方形PCGQ的顶点P也在⊙O上,若BC=1,GH=2,则正方形PCGQ的面积为( )