题目内容
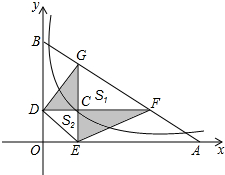 如图,已知动点C在函数y=
如图,已知动点C在函数y=| 6 |
| x |
| 4 |
| 3 |
考点:反比例函数系数k的几何意义
专题:
分析:作GH⊥y轴于H.设C(a,
),CF=m,CG=n,BH=t,则BD=n+t.先由S阴影部分=
S△BGD,得出
an+
×
m=
×
a(n+t),即an+
m=
a(n+t)①,由△BHG∽△GCF,根据相似三角形对应边成比例得出
=
,即an=mt,m=
②,由tan∠DEO=tan∠GFC,得出
=
,即an=m•
③,比较②③,得t=
,at=6④,再将②④代入①,求出an=12,然后得到S1=
mn=
×
×n=
×
×n=
×
=
×
=12,S2=
×6=3,进而求出S1+S2=15.
| 6 |
| a |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| a |
| 4 |
| 3 |
| 1 |
| 2 |
| 6 |
| a |
| 4 |
| 3 |
| t |
| n |
| a |
| m |
| an |
| t |
| ||
| a |
| n |
| m |
| 6 |
| a |
| 6 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| an |
| t |
| 1 |
| 2 |
| an | ||
|
| 1 |
| 2 |
| (an)2 |
| 6 |
| 1 |
| 2 |
| 144 |
| 6 |
| 1 |
| 2 |
解答: 解:如图,作GH⊥y轴于H.
解:如图,作GH⊥y轴于H.
设C(a,
),CF=m,CG=n,BH=t,则BD=n+t.
∵S阴影部分=
S△BGD,
∴
an+
×
m=
×
a(n+t),
即an+
m=
a(n+t)①.
∵△BHG∽△GCF,
∴
=
,即
=
,
∴an=mt,m=
②.
∵∠DEO=∠BAO=∠GFC,
∴tan∠DEO=tan∠GFC,
∴
=
,
∴an=m•
③,
比较②③,得mt=m•
,
∴t=
,at=6④,
将②④代入①,得an+
×
=
an+
×6,
∴
=
an+8,
∴
=
an+8,即an=
an+8,
∴
an=8,
∴an=12.
∵S1=
mn=
×
×n=
×
×n=
×
=
×
=12,
S2=
×6=3,
∴S1+S2=12+3=15.
故答案为15.
 解:如图,作GH⊥y轴于H.
解:如图,作GH⊥y轴于H.设C(a,
| 6 |
| a |
∵S阴影部分=
| 4 |
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| a |
| 4 |
| 3 |
| 1 |
| 2 |
即an+
| 6 |
| a |
| 4 |
| 3 |
∵△BHG∽△GCF,
∴
| BH |
| GC |
| GH |
| FC |
| t |
| n |
| a |
| m |
∴an=mt,m=
| an |
| t |
∵∠DEO=∠BAO=∠GFC,
∴tan∠DEO=tan∠GFC,
∴
| ||
| a |
| n |
| m |
∴an=m•
| 6 |
| a |
比较②③,得mt=m•
| 6 |
| a |
∴t=
| 6 |
| a |
将②④代入①,得an+
| 6 |
| a |
| an |
| t |
| 4 |
| 3 |
| 4 |
| 3 |
∴
| 6n |
| t |
| 1 |
| 3 |
∴
| 6n | ||
|
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 2 |
| 3 |
∴an=12.
∵S1=
| 1 |
| 2 |
| 1 |
| 2 |
| an |
| t |
| 1 |
| 2 |
| an | ||
|
| 1 |
| 2 |
| (an)2 |
| 6 |
| 1 |
| 2 |
| 144 |
| 6 |
S2=
| 1 |
| 2 |
∴S1+S2=12+3=15.
故答案为15.
点评:本题考查了反比例函数系数k的几何意义,三角形的面积,相似三角形的判定与性质,锐角三角函数的定义,有一定难度.本题对式子的变形能力有较高要求.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图,A、B、C是⊙O上的三点,且∠ABD=70°,AB=BD,则∠O的度数是( )
如图,A、B、C是⊙O上的三点,且∠ABD=70°,AB=BD,则∠O的度数是( )| A、70° | B、110° |
| C、130° | D、140° |
 如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是
如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是
 如图为二次函数y=ax2+bx+c的图象,有下列说法:
如图为二次函数y=ax2+bx+c的图象,有下列说法:
