Question

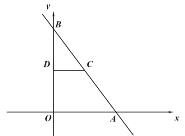
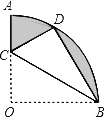
【题目】已知，平面直角坐标系中，直线y=-x+6交x轴于点A，交y轴于点B，点C为OB上一点，连接AC，且；

（1）求C点坐标；

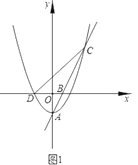
（2）D为OC上一点，连接AD并延长至点E，连接OE、CE，取AE中点F，连接BF、OF，当F在第一象限时，求的值；

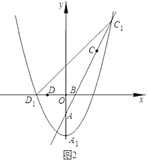
（3）在（2）的条件下，将射线AC延AE翻折交OE于点P，连接BP，过O作OH⊥AE于H，若AD=4FH，，求直线PB的解析式．

Answer 1

【答案】（1）；（2）9；（3）

【解析】

（1）作，证得是等腰直角三角形，设CR=BR=，由已知得，根据勾股定理列出等式即可求解；

（2）作于，取中点，连接交于，根据三角形中位线定理，即可得出结论；

（3）延长交轴于，取中点，连接，作交于，，交EO延长线于点M，设，，根据勾股定理及锐角三角函数求得有关线段，证得，得到，设，设法求得，，从而求得点S的坐标，利用待定系数法即可求解．

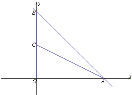
（1）作，如图：

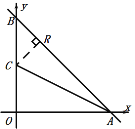
令y=0，则x=6，令x=0，则y=6，

∴点AB的坐标分别为(6，0)，(0，6)

∴OA=6，OB=6，

∴，

∵OA=OB =6，

∴∠OBA=45，

∴是等腰直角三角形，

设CR=BR=，

∵，

∴，

∴，

解得：，

∴，

∴，

∴C点坐标为：；

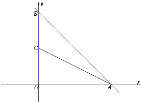
（2）作于，取中点，连接交于，

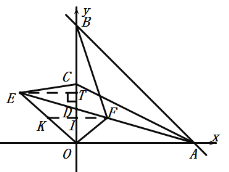
∵K是OE的中点，F是AE的中点，

∴KF∥OA，，

∵，

∴ET∥KF∥OA，

∴，

∴；

（3）延长交轴于，取中点，连接，作交于，，交EO延长线于点M，

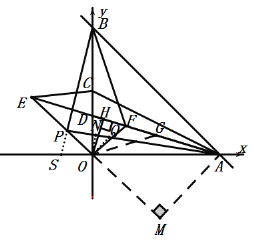
设，则，

∴，

设，

∴，

∴，

∵OH⊥AE于H，

∴，

∴，即，

即，

∴，

解得：，

∴，

，

由勾股定理得，

∴，，

∵

∴，

设，

∴，

∵，

∴，

∴，

又∵，

∴，

∵，

∴，又，，

∴，

∴，

设，，，，，

∵，且，

∴，

∴，

∵，

，

∴，，

∵，

∴，

∴，

∴，

∴，

∴点S的坐标为(-，0)，

设直线PB的解析式为，

把S (-，0)代入得：，

∴直线PB的解析式为