Question

【题目】如图,在△ABC中,∠ACB=120°，BC=4，D为AB的中点，DC⊥BC，则△ABC的面积是___.

Answer 1

【答案】8.

【解析】

根据垂直的定义得到∠BCD=90°，延长CD到H使DH=CD，由线段中点的定义得到AD=BD，根据全等三角形的性质得到AH=BC=4，∠H=∠BCD=90°，求得CD=2，于是得到结论．

解：∵DC⊥BC，

∴∠BCD=90°，

∵∠ACB=120°，

∴∠ACD=30°，

延长CD到H使DH=CD，

∵D为AB的中点，

∴AD=BD，

在△ADH与△BCD中， ，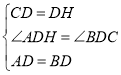
∴△ADH≌△BCD（SAS），

∴AH=BC=4，∠H=∠BCD=90°，

∵∠ACH=30°，

∴CH=AH=4，

∴CD=2，

∴△ABC的面积=2S△BCD=2××4×2=8，
故答案为：8．