题目内容
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:

①b2﹣4ac>0;
②2a+b<0;
③4a﹣2b+c=0;
④a:b:c=﹣1:2:3.
其中正确的个数是( )
A.1 B.2 C.3 D.4
B.
【解析】
试题分析:∵二次函数y=ax2+bx+c(a≠0)的图象和x轴有两个交点,
∴b2-4ac>0,∴①正确;
∵二次函数的对称轴是直线x=1,
即二次函数的顶点的横坐标为x=- =1,
=1,
∴2a+b=0,∴②错误;
把x=-2代入二次函数的解析式得:y=4a-2b+c,
从图象可知,当x=-2时,y<0,
即4a-2b+c<0,∴③错误;
∵二次函数的图象和x轴的一个交点时(-1,0),对称轴是直线x=1,
∴另一个交点的坐标是(3,0),
∴设y=ax2+bx+c=a(x-3)(x+1)=ax2-2ax-3a,
即a=a,b=-2a,c=-3a,
∴a:b:c=a:(-2a):(-3a)=-1:2:3,
∴④正确;
故选B.
考点:二次函数图象与系数的关系.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目

 满足
满足 ,那么我们称这个方程为“凤凰”方程.已知方程
,那么我们称这个方程为“凤凰”方程.已知方程
 B.
B. C.
C. D.
D.
 与水平距离
与水平距离 之间的关系为
之间的关系为 ,由此可知铅球推出的距离是
,由此可知铅球推出的距离是  .
.
 ≥0,所以
≥0,所以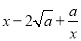 ≥0,从而
≥0,从而 (当
(当 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当
,由上述结论可知:当 .
. ,则当x= 1 时,y1+y2取得最小值为 2 .
,则当x= 1 时,y1+y2取得最小值为 2 . ,求
,求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
 。台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处。因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西600方向继续移动,以O为原点建立如图所示的直角坐标系。
。台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处。因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西600方向继续移动,以O为原点建立如图所示的直角坐标系。
 B、
B、 C、
C、 D、
D、