题目内容
已知（2x-21）（3x-7）-（3x-7）（x-13）可分解因式为（3x+a）（x+b），其中a，b均为整数，则a+3b= ，ab ．
考点：因式分解-提公因式法
专题：
分析：首先提取公因式，进而合并同类项得出a，b的值，进而得出答案．
解答：解：∵（2x-21）（3x-7）-（3x-7）（x-13）
=（3x-7）（2x-21-x+13）
=（3x-7）（x-8），
=（3x+a）（x+b），
∴a=-7，b=-8，
故a+3b=-7-24=-31，
ab=56．
故答案为：-31，56．
=（3x-7）（2x-21-x+13）
=（3x-7）（x-8），
=（3x+a）（x+b），
∴a=-7，b=-8，
故a+3b=-7-24=-31，
ab=56．
故答案为：-31，56．
点评：此题主要考查了提取公因式法的应用，正确提取公因式是解题关键．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
关于单项式（-5）2x3y，下列说法正确的是（ ）
| A、次数是6 | B、系数是-5 |
| C、次数是3 | D、系数是25 |
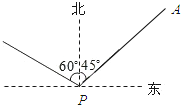如图，某港口P位于东西方向的海岸线上，小岛A在港口P的北偏东45°方向上，距离港口80海里，“远航”号从A出发，沿AP方向以10海里/小时的速度驶向港口，“海天”号从港口P出发，沿北偏西60°方向，以20海里/小时的速度驶离港口，现两船同时出发，试问出发几小时，“海天”号在“远航”号的正西方向？（