题目内容
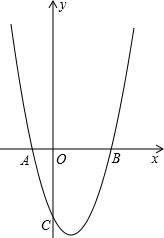 如图,抛物线y=ax2+bx-3交x轴于点A(-1,0),B(3,0)两点,交y轴于点C.
如图,抛物线y=ax2+bx-3交x轴于点A(-1,0),B(3,0)两点,交y轴于点C.(1)求抛物线的解析式;
(2)在第一象限内抛物线上,找一点M使△OCM的面积是△OAM的面积的
| 3 |
| 2 |
(3)在抛物线上,找一点N使∠NCA=2∠ACB,求点N的坐标.
考点:二次函数综合题
专题:
分析:(1)把A(-1,0),B(3,0)两点代入y=ax2+bx-3求解即可,
(2)由y=x2-2x-3交y轴于点C.可得OC=3,设M(x,y),由△OCM的面积是△OAM的面积的
倍,可得
OC•x=
×
•|AO|•y,解得y=2x,代入y=x2-2x-3求解即可.
(3)作NQ⊥AB于点Q,CH⊥NQ于点H,由△AOC∽△NHC,设N(x,y),由
=
,可得x=-3y-9,与y=x2-2x-3联立求解即可.
(2)由y=x2-2x-3交y轴于点C.可得OC=3,设M(x,y),由△OCM的面积是△OAM的面积的
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
(3)作NQ⊥AB于点Q,CH⊥NQ于点H,由△AOC∽△NHC,设N(x,y),由
| NH |
| AO |
| CH |
| CO |
解答:解:(1)把A(-1,0),B(3,0)两点代入y=ax2+bx-3得
,解得
,
所以抛物线的解析式y=x2-2x-3.
(2)如图1,
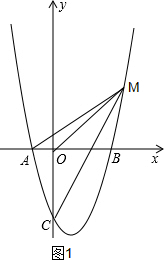
∵y=x2-2x-3交y轴于点C.
∴OC=3,
设M(x,y),
∵△OCM的面积是△OAM的面积的
倍,
∴
OC•x=
×
•|AO|•y,
∴y=2x,
代入y=x2-2x-3得,x1=2+
,x2=2-
(舍去),
∴y=2x=4+2
,
∴M(2+
,4+2
).
(3)如图2,作NQ⊥AB于点Q,CH⊥NQ于点H,
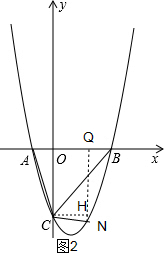
∵OB=3,OC=3,
∴∠OCB=∠BCH=45°,
∵∠NCA=2∠ACB,
∴∠OCA=∠NCH,∠AOC=∠NHC=90°,
∴△AOC∽△NHC,
设N(x,y),
∴
=
,
∴
=
,解得x=-3y-9,
与y=x2-2x-3联立得
,解得
(舍去),
.
∴N((
,-
).
|
|
所以抛物线的解析式y=x2-2x-3.
(2)如图1,

∵y=x2-2x-3交y轴于点C.
∴OC=3,
设M(x,y),
∵△OCM的面积是△OAM的面积的
| 3 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴y=2x,
代入y=x2-2x-3得,x1=2+
| 7 |
| 7 |
∴y=2x=4+2
| 7 |
∴M(2+
| 7 |
| 7 |
(3)如图2,作NQ⊥AB于点Q,CH⊥NQ于点H,

∵OB=3,OC=3,
∴∠OCB=∠BCH=45°,
∵∠NCA=2∠ACB,
∴∠OCA=∠NCH,∠AOC=∠NHC=90°,
∴△AOC∽△NHC,
设N(x,y),
∴
| NH |
| AO |
| CH |
| CO |
∴
| -y-3 |
| 1 |
| x |
| 3 |
与y=x2-2x-3联立得
|
|
|
∴N((
| 5 |
| 3 |
| 32 |
| 9 |
点评:本题主要考查了二次函数的综合题,解题的关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
下列说法正确的有( )个
①任何数的0次幂都等于1.
②同底数幂相乘,底数不变,指数相加.
③有一个角是60°的三角形是等边三角形.
④到三角形三个顶点距离相等的点是三角形三条中线的交点.
⑤到三角形三个顶点距离相等的点是三角形三边垂直平分线的交点.
①任何数的0次幂都等于1.
②同底数幂相乘,底数不变,指数相加.
③有一个角是60°的三角形是等边三角形.
④到三角形三个顶点距离相等的点是三角形三条中线的交点.
⑤到三角形三个顶点距离相等的点是三角形三边垂直平分线的交点.
| A、1个 | B、2个 | C、3个 | D、4个 |
如图,羊字象征吉祥和美满,如图的图案与羊有关,其中是轴对称的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
已知
+|b-1|=0,那么(a+b)2014的值为( )
| a+2 |
| A、1 |
| B、-1 |
| C、-32014 |
| D、32014 |
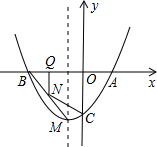 如图,y=ax2+bx-2的图象过A(1,0),B(-2,0)与y轴交于点C.
如图,y=ax2+bx-2的图象过A(1,0),B(-2,0)与y轴交于点C.