题目内容
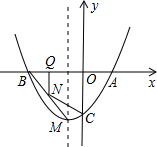 如图,y=ax2+bx-2的图象过A(1,0),B(-2,0)与y轴交于点C.
如图,y=ax2+bx-2的图象过A(1,0),B(-2,0)与y轴交于点C.(1)求抛物线关系式及顶点M的坐标;
(2)若N为线段BM上一点,过N作x轴的垂涎,垂足为Q,当N在线段BM上运动(N不与点B、点M重合),设NQ的长为t,四边形NQAC的面积为S,求S与t的关系式并求出S的最大值;
(3)在抛物线的对称轴上是否存在点P,使△PAC为直角三角形?若存在,请求出所有符合条件P的坐标.
考点:二次函数综合题
专题:
分析:(1)利用交点式得出抛物线的解析式为y=a(x-1)(x+2),将C(0,-2)坐标代入求出a的值即可;
(2)利用待定系数法求出线段BM所在的直线的解析式,再利用S=S△AOC+S梯形OCNQ求出S与t间的函数关系式即可求出最值;
(3)利用①若∠APC=90°,则PC2+PA2=AC2,②若∠ACP=90°,则PC2+AC2=PA2,③若∠PAC=90°,则AC2+PA2=PC2,分别求出m的值即可得出P点坐标.
(2)利用待定系数法求出线段BM所在的直线的解析式,再利用S=S△AOC+S梯形OCNQ求出S与t间的函数关系式即可求出最值;
(3)利用①若∠APC=90°,则PC2+PA2=AC2,②若∠ACP=90°,则PC2+AC2=PA2,③若∠PAC=90°,则AC2+PA2=PC2,分别求出m的值即可得出P点坐标.
解答:解:(1)∵二次函数y=ax2+bx-2的图象经过点A(1,0)及B(-2,0)两点.
∴设抛物线的解析式为y=a(x-1)(x+2),将C(0,-2)坐标代入,-2=a(0-1)(0+2),
解得:a=1,
故y=x2+x-2=(x+
)2-
;则其顶点M的坐标是(-
,-
);
(2)设线段BM所在直线的解析式为y=kx+b,
∴
,
解得:
,
∴线段BM所在的直线的解析式为y=-
x-3,
∵-t=-
x-3,
∴x=
t-2,
点N的坐标为N(
t-2,-t),
∴S=S△AOC+S梯形OCNQ=
×1×2+
(2+t)•|
t-2|═-
t2+
t+3,
∴S与t间的函数关系式为S=-
t2+
t+3=-
(t-
)2+
,
当t=
时,S的最大值为
;
(3)存在符合条件的点P,
设点P的坐标为P(-
,m),如图,连接PA、PC,作CE⊥MP于E.
则AC2=12+22=5,
PA2=(-
-1)2+m2,PC2=(
)2+(m+2)2,
分以下几种情况讨论:
①若∠APC=90°,则PC2+PA2=AC2,
即(-
-1)2+m2+(
)2+(m+2)2=5,
解得:m1=-
,m2=-
,
②若∠ACP=90°,则PC2+AC2=PA2,
即(
)2+(m+2)2+5=(-
-1)2+m2,
解得:m=-
.
③若∠PAC=90°,则AC2+PA2=PC2,(-
-1)2+m2+5=(
)2+(m+2)2,
解得:m=
,
综上所述,存在满足条件的点P,其坐标分别是:P1(-
,-
),P2(-
,-
),P1(-
,-
),P1(-
,
).
∴设抛物线的解析式为y=a(x-1)(x+2),将C(0,-2)坐标代入,-2=a(0-1)(0+2),
解得:a=1,
故y=x2+x-2=(x+
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
(2)设线段BM所在直线的解析式为y=kx+b,
∴
|
解得:
|
∴线段BM所在的直线的解析式为y=-
| 3 |
| 2 |
∵-t=-
| 3 |
| 2 |
∴x=
| 2 |
| 3 |
点N的坐标为N(
| 2 |
| 3 |
∴S=S△AOC+S梯形OCNQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴S与t间的函数关系式为S=-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 37 |
| 12 |
当t=
| 1 |
| 2 |
| 37 |
| 12 |
(3)存在符合条件的点P,
设点P的坐标为P(-
| 1 |
| 2 |

则AC2=12+22=5,
PA2=(-
| 1 |
| 2 |
| 1 |
| 2 |
分以下几种情况讨论:
①若∠APC=90°,则PC2+PA2=AC2,
即(-
| 1 |
| 2 |
| 1 |
| 2 |
解得:m1=-
| 1 |
| 2 |
| 3 |
| 2 |
②若∠ACP=90°,则PC2+AC2=PA2,
即(
| 1 |
| 2 |
| 1 |
| 2 |
解得:m=-
| 7 |
| 4 |
③若∠PAC=90°,则AC2+PA2=PC2,(-
| 1 |
| 2 |
| 1 |
| 2 |
解得:m=
| 3 |
| 4 |
综上所述,存在满足条件的点P,其坐标分别是:P1(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题考查了二次函数的综合应用以及勾股定理的应用等知识,注意△PAC为直角三角形时,应该分三种情况进行讨论,以防漏解.

练习册系列答案
相关题目
某商店先进货7辆自行车,平均每辆自行车a元,后来又进货5辆自行车,平均每辆自行车b元,后来商店以每辆
的价格把自行车全部卖掉了,结果发现赔了钱,赔钱的原因是( )
| a+b |
| 2 |
| A、a=b | B、a<b |
| C、与a、b的大小无关 | D、a>b |
已知二次函数y=3(x-1)2+k的图象上有A(
,y1)、B(2,y2)、C(-5,y3)三个点,则y1、y2、y3的大小关系是( )
| 2 |
| A、y3>y2>y1 |
| B、y2>y1>y3 |
| C、y3>y1>y2 |
| D、y1>y2>y3 |
2012年国内生产总值为47.2万亿元,数据47.2万亿精确到( )
| A、千亿位 | B、亿位 |
| C、千位 | D、十分位 |
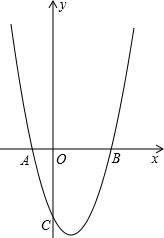 如图,抛物线y=ax2+bx-3交x轴于点A(-1,0),B(3,0)两点,交y轴于点C.
如图,抛物线y=ax2+bx-3交x轴于点A(-1,0),B(3,0)两点,交y轴于点C.