题目内容
小红在做一道题：已知两个多项式A，B，A=x2+3x-5，计算A+2B时，她误将A+2B写成2A+B，算出的结果是x2+8x-7．请你帮她计算出正确结果．
考点：整式的加减
专题：计算题
分析：根据2A+B的结果及A，确定出B，列出正确的算式，去括号合并即可得到结果．
解答：解：∵2A+B=x2+8x-7，即2（x2+3x-5）+B=x2+8x-7，
∴B=（x2+8x-7）-2（x2+3x-5）=x2+8x-7-2x2-6x+10=-x2+2x+3，
则A+2B=（x2+8x-7）+2（-x2+2x+3）=x2+8x-7-2x2+4x+6=-x2+7x+1．
∴B=（x2+8x-7）-2（x2+3x-5）=x2+8x-7-2x2-6x+10=-x2+2x+3，
则A+2B=（x2+8x-7）+2（-x2+2x+3）=x2+8x-7-2x2+4x+6=-x2+7x+1．
点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
下面的计算正确的是（ ）
| A、6a-5a=1 |
| B、2（a+b）=2a+b |
| C、-（a-b）=-a+b |
| D、-2（3x-1）=-6x-2 |
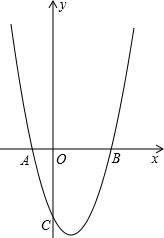如图，抛物线y=ax2+bx-3交x轴于点A（-1，0），B（3，0）两点，交y轴于点C．
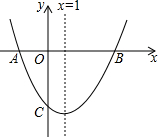如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．已知二次函数y=3（x-1）2+k的图象上有A（
，y1）、B（2，y2）、C（-5，y3）三个点，则y1、y2、y3的大小关系是（ ）
| 2 |
| A、y3＞y2＞y1 |
| B、y2＞y1＞y3 |
| C、y3＞y1＞y2 |
| D、y1＞y2＞y3 |
