题目内容
一直角三角形的一直角边长为6，斜边长比另一直角边长大2，则斜边的长为（ ）
| A、4 | B、6 | C、8 | D、10 |
考点：勾股定理
专题：
分析：设另一条直角边为a，则斜边为（a+2），再根据勾股定理求出a的值即可．
解答：解：另一条直角边为a，则斜边为（a+2）．
∵另一直角边长为6，
∴（a+2）2=a2+62，解得a=8，
∴a+2=8+2=10．
故选：D．
∵另一直角边长为6，
∴（a+2）2=a2+62，解得a=8，
∴a+2=8+2=10．
故选：D．
点评：本题考查的是勾股定理，根据题意设出直角三角形的斜边及直角边的长是解答此题的关键．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
如图，D、E、F分别是△ABC各边的中点．如果△ABC∽△A1B1C1，AB等5，A1B1等于15，那么△ABC的周长和△A1B1C1的周长之比是（ ）
| A、1：3 | B、2：3 |
| C、4：9 | D、3：2 |
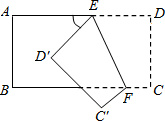如图所示，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置．若∠AED′=50°，则∠DEF等于（ ）| A、50° | B、65° |
| C、75° | D、60° |
下列代数式书写正确的是（ ）
| A、a48 | ||
| B、x÷y | ||
| C、3（x+y） | ||
D、1
|
如果x+
，那么x的取值范围是（ ）
| x+1 |
| A、x=0 | B、x=1 |
| C、x≥-1 | D、x=0或x=1 |
在
=
+
中，用u、v表示f，正确的是（ ）
| 1 |
| f |
| 1 |
| u |
| 1 |
| v |
A、
| ||
B、
| ||
| C、u+v | ||
| D、uv |
已知，∠1与∠2互为邻补角，∠1=140°，则∠2的余角的度数为（ ）
| A、30° | B、40° |
| C、50° | D、100° |