题目内容
如果反比例函数y=-
的图象过点(x1,y1),(x2,y2),(x3,y3),且x1>x2>0>x3,那么y1,y2,y3的大小关系是( )
| k2+1 |
| x |
| A、y3>y1>y2 |
| B、y3>y2>y1 |
| C、y1>y2>y3 |
| D、y2>y1>y3 |
考点:反比例函数图象上点的坐标特征
专题:
分析:由于-(k2+1)<0,根据反比例函数性质得反比例函数图象分布在第二、四象限,所以x1>x2>0>x3时,那么0>y1>y2,y3>0.
解答:解:∵-(k2+1)<0,
∴反比例函数图象分布在第二、四象限,
∴x1>x2>0>x3时,那么0>y1>y2,y3>0,
∴y3>y1>y2.
故选A.
∴反比例函数图象分布在第二、四象限,
∴x1>x2>0>x3时,那么0>y1>y2,y3>0,
∴y3>y1>y2.
故选A.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数的性质.
| k |
| x |

练习册系列答案
相关题目
如果x=3,y=4适合解析式y=
,那么下列也适合y=
的一组数据是( )
| m2-1 |
| x |
| m2-1 |
| x |
| A、x=2,y=6 |
| B、x=-2,y=6 |
| C、x=4,y=-3 |
| D、x=3,y=-4 |
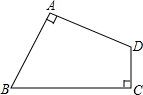 在四边形ABCD中,∠A=∠C=90°,AB=AD.若BC+CD=8,则四边形ABCD的面积是( )
在四边形ABCD中,∠A=∠C=90°,AB=AD.若BC+CD=8,则四边形ABCD的面积是( )| A、16 | B、32 | C、48 | D、64 |
关于x的方程mx2-2(3m-1)x+9m-1=0有两个实数根,那么m的取值范围是( )
A、m≤
| ||
B、0<m<
| ||
C、m≤
| ||
D、m≥
|
一条圆弧所对的圆心角等于240°,它的长度等于半径为4cm的圆的周长,则这条弧所在的半径为( )
| A、3cm | B、4cm |
| C、5cm | D、6cm |
如果反比例函数的图象经过点(-
,
),那么它的图象在( )
| 2 |
| 3 |
| A、第二象限 | B、一、三象限 |
| C、二、四象限 | D、二、三象限 |
已知二次函数y=3x2+k的图象上有三点A(1,y1),B(2,y2),C(-3,y3),则y1,y2,y3的大小关系为( )
| A、y1>y2>y3 |
| B、y2>y1>y3 |
| C、y3>y1>y2 |
| D、y3>y2>y1 |
 如图,在△ABC中,∠C=90°,AC=2,tanA=3,则BC=
如图,在△ABC中,∠C=90°,AC=2,tanA=3,则BC=