题目内容
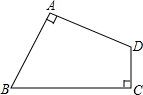 在四边形ABCD中,∠A=∠C=90°,AB=AD.若BC+CD=8,则四边形ABCD的面积是( )
在四边形ABCD中,∠A=∠C=90°,AB=AD.若BC+CD=8,则四边形ABCD的面积是( )| A、16 | B、32 | C、48 | D、64 |
考点:全等三角形的判定与性质
专题:
分析:将BC+CD=8进行平方运算,然后根据等腰直角三角形的面积=
结合四边形ABCD的面积表达式即可得出答案.
| 斜边2 |
| 4 |
解答:解:连接BD,
∵∠A=90°,
∴AB2+AD2=BD2.
∵AB=AD.
∴2AD2=BD2.
∴AD2=
BD2.
∵S四边形ABCD=SABD+SBCD=
BC•CD+
AB×AD=
BC•CD+
AB2
∴S四边形ABCD=
BC•CD+
BD2.
∴4S四边形ABCD=2BC•CD+BD2.
∵BC+CD=8,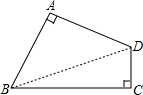
∴BC2+CD2+2BC×CD=64.
∵∠C=90°,
∴BC2+CD2=BD2,
∴BD2+2BC×CD=64
∴4S四边形ABCD=64,
∴S四边形ABCD=16.
故选A.
∵∠A=90°,
∴AB2+AD2=BD2.
∵AB=AD.
∴2AD2=BD2.
∴AD2=
| 1 |
| 2 |
∵S四边形ABCD=SABD+SBCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 4 |
∴4S四边形ABCD=2BC•CD+BD2.
∵BC+CD=8,

∴BC2+CD2+2BC×CD=64.
∵∠C=90°,
∴BC2+CD2=BD2,
∴BD2+2BC×CD=64
∴4S四边形ABCD=64,
∴S四边形ABCD=16.
故选A.
点评:本题考查了三角形的面积公式的运用,勾股定理的运用,完全平方公式的运用,解答时求出根据勾股定理求解是关键.

练习册系列答案
相关题目
当x<-3时,化简
+
的结果是( )
| (2x-1)2 |
| (x+3)2 |
| A、-3x-2 | B、4-x |
| C、x-4 | D、3x+2 |
下列等式成立的是( )
A、
| ||||||||
B、
| ||||||||
C、a
| ||||||||
D、
|
如果反比例函数y=-
的图象过点(x1,y1),(x2,y2),(x3,y3),且x1>x2>0>x3,那么y1,y2,y3的大小关系是( )
| k2+1 |
| x |
| A、y3>y1>y2 |
| B、y3>y2>y1 |
| C、y1>y2>y3 |
| D、y2>y1>y3 |
对于反比例函数y=
,当自变量x的值从3增加到6时,函数值减少了1,则函数的解析式为( )
| k |
| x |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
使式子
有意义的x的取值范围是( )
| ||
| x-2 |
| A、x≠2 |
| B、x>-3且x≠2 |
| C、x≥3且x≠2 |
| D、x≥-3且x≠2 |
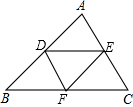 如图,在△ABC中,D,E,F分别在△ABC的三边上,且DE∥BC,DF∥AC,EF∥AB,则图中平行四边形有( )
如图,在△ABC中,D,E,F分别在△ABC的三边上,且DE∥BC,DF∥AC,EF∥AB,则图中平行四边形有( )| A、4个 | B、3个 | C、2个 | D、1个 |
 如图,在平行四边形ABCD中,∠B=60°,AB=3,BC=4,E为BC的中点,EF⊥AB于F,交DC的延长线于G,连接DF,DE,则S△DEF=
如图,在平行四边形ABCD中,∠B=60°,AB=3,BC=4,E为BC的中点,EF⊥AB于F,交DC的延长线于G,连接DF,DE,则S△DEF=