题目内容
4.已知点P是一次函数y=-2x+8的图象上的一点,如果图象与x轴交于Q点,且△OPQ的面积等于8,求点P的坐标.分析 先求出Q点坐标,根据一次函数图象上点的坐标特征设P(x,-2x+8),则根据三角形面积公式得到$\frac{1}{2}$•4•|-2x+8|=8,然后解方程求出x即可得到P点坐标.
解答 解:当y=0时,-2x+8=0,解得x=4,则Q(4,0),
设P(x,-2x+8),
所以$\frac{1}{2}$•4•|-2x+8|=8,解得x=2或x=6,
所以P点坐标为(2,4)或(6,-4).
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
15.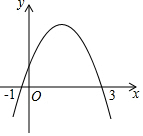 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则下列结论中正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则下列结论中正确的是( )
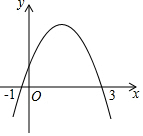 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则下列结论中正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图,则下列结论中正确的是( )| A. | a>0 | B. | b<0 | C. | c<0 | D. | a+b+c>0 |
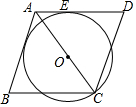 如图,点O在菱形ABCD的对角线AC上,以OC为半径的⊙O与边AD相切于点E.
如图,点O在菱形ABCD的对角线AC上,以OC为半径的⊙O与边AD相切于点E.