题目内容
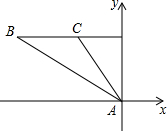 某海关缉查艇在A处发现一艘可疑船只在其正北方向,以每小时20海里向正西方向逃窜,2小时后到达A的北偏西45°,此时缉查艇马上行动,沿北偏西60°方向进行拦截,一段时间后恰好在B处截获可疑船只,试求出缉查艇的速度.(精确到0.1海里)
某海关缉查艇在A处发现一艘可疑船只在其正北方向,以每小时20海里向正西方向逃窜,2小时后到达A的北偏西45°,此时缉查艇马上行动,沿北偏西60°方向进行拦截,一段时间后恰好在B处截获可疑船只,试求出缉查艇的速度.(精确到0.1海里)
解:设BC交AD于点D,
由题意可知∠BAE=∠ABD=30°,∠CAD=∠DCA=45°,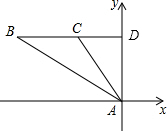
在Rt△ADC中,∵∠ADC=90°,∠DAC=45°,AC=20×2=40海里,
∴AD=20 海里,
海里,
在Rt△ADB中,∠ADB=90°,∠DBA=30°,
∴AB=2AD=40 海里,
海里,
∴缉查艇的速度约为 =20
=20 ≈28.3海里/小时.
≈28.3海里/小时.
答:缉查艇的速度约为28.3海里/小时.
分析:根据题意求出AB的距离,根据路程、速度、时间的关系即可求出缉查艇的速度.
点评:本题考查了解直角三角形的应用-方向角问题,难度中等,正确作辅助线构建直角三角形是解题的关键.
由题意可知∠BAE=∠ABD=30°,∠CAD=∠DCA=45°,

在Rt△ADC中,∵∠ADC=90°,∠DAC=45°,AC=20×2=40海里,
∴AD=20
 海里,
海里,在Rt△ADB中,∠ADB=90°,∠DBA=30°,
∴AB=2AD=40
 海里,
海里,∴缉查艇的速度约为
 =20
=20 ≈28.3海里/小时.
≈28.3海里/小时.答:缉查艇的速度约为28.3海里/小时.
分析:根据题意求出AB的距离,根据路程、速度、时间的关系即可求出缉查艇的速度.
点评:本题考查了解直角三角形的应用-方向角问题,难度中等,正确作辅助线构建直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,A点、B点分别表示小岛码头、海岸码头的位置,离B点正东方向的7.00km处有一海岸瞭望塔C,又用经纬仪测出:A点分别在B点的北偏东57°处、在C点的东北方向.
如图,A点、B点分别表示小岛码头、海岸码头的位置,离B点正东方向的7.00km处有一海岸瞭望塔C,又用经纬仪测出:A点分别在B点的北偏东57°处、在C点的东北方向.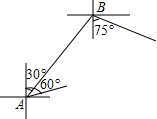 如图,在一次海上联合作战演习中,红方一艘侦察艇在A处发现在其北偏东30°方向,相距12海里的B处水面上,有蓝方一艘小艇正以每小时8海里的速度沿南偏东75°方向前进.若侦察艇以每小时16海里的速度,沿北偏东60°方向拦截蓝方的小艇.试问能否成功拦截?(
如图,在一次海上联合作战演习中,红方一艘侦察艇在A处发现在其北偏东30°方向,相距12海里的B处水面上,有蓝方一艘小艇正以每小时8海里的速度沿南偏东75°方向前进.若侦察艇以每小时16海里的速度,沿北偏东60°方向拦截蓝方的小艇.试问能否成功拦截?(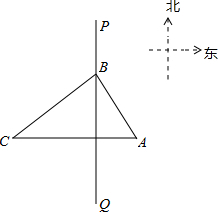 B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?
B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?