题目内容
如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知下在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,A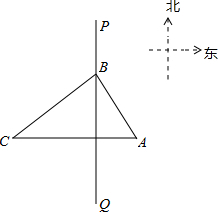 B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?
B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?
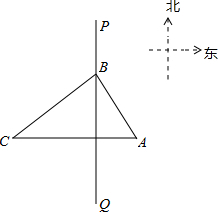 B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?
B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?分析:根据勾股定理的逆定理可得出△ABC是直角三角形,从而判定△CBD∽△CAB,然后利用相似三角形的性质可求出CD的长度,也可求出进入我领海的时间.
解答:解:
∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,即△ABC是直角三角形,
从而可判断△CBD∽△CAB,
故可得
=
,
解得:CD=
=6.4,
又∵该船只的速度为12.8海里/小时,
∴需要
=0.5小时=30分进入我领海.
即最早晚上10时58分进入我领海.

∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,即△ABC是直角三角形,
从而可判断△CBD∽△CAB,
故可得
| BC |
| AC |
| CD |
| CB |
解得:CD=
| 32 |
| 5 |
又∵该船只的速度为12.8海里/小时,
∴需要
| 6.4 |
| 12.8 |
即最早晚上10时58分进入我领海.
点评:此题考查了勾股定理及勾股定理逆定理的知识,解答本题的关键是判断出△ABC是直角三角形,利用相似三角形的性质进行解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

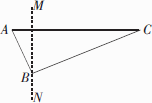

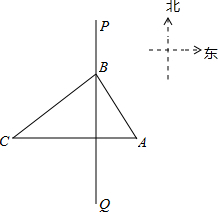 B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?
B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?