题目内容
如图，A点、B点分别表示小岛码头、海岸码头的位置，离B点正东方向的7.00km处有一海岸瞭望塔C，又用经纬仪测出：A点分别在B点的北偏东57°处、在C点的东北方向．
（1）试求出小岛码头A点到海岸线BC的距离；
（2）有一观光客轮K从B至A方向沿直线航行：
①某瞭望员在C处发现，客轮K刚好在正北方向的D处，试求出客轮驶出的距离BD的长；
②当客轮航行至E处时，发现E点在C的北偏东27°处,请求出E点到C点的距离；
（注：tan33°≈0.65，sin33°≈0.54，cos33°≈0.84，结果精确到0.01km）
【答案】
（1）13.00km；（2）①8.33km；②7.56km
【解析】
试题分析：（1）过A作AM⊥BC于M，设AM=x，由∠ACM=45°可得CM=x，再根据33°角的正切函数列方程求解即可；
（2）①根据33°角的余弦函数列方程求解即可；
②过C作CN⊥AB于N，根据33°角的正弦函数列方程求解即可.
（1）过A作AM⊥BC于M，
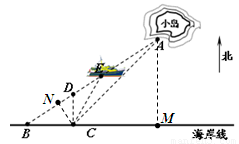
设AM=x，
∵∠ACM=45°，
∴CM=x
则由题意得：tan33°=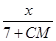
=
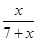
∴(7＋x)tan33°=x
则7×tan33°=x(1－tan33°)
7×0.65≈0.35x
∴x≈13.00(km)；
（2）①∵cos33°=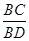
=
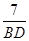
∴BD=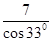
≈8.33(km)
②过C作CN⊥AB于N，
∵∠ABC=33°，∠BEC=30°，
∴sin33°=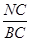
·
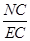=sin30°="0.5"
则EC=2NC=2BC×sin33°≈2×7×0.54≈7.56(km).
考点：解直角三角形的应用
点评：解直角三角形的应用是中考必考题，一般难度不大，正确作出辅助线构造直角三角形是解题关键.
练习册系列答案
相关题目
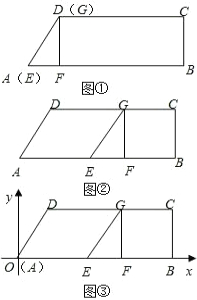如图①，在梯形ABCD中，CD∥AB，∠ABC=90°，∠DAB=60°，AD=2，CD=4．另有一直角三角形EFG，∠EFG=90°，点G与点D重合，点E与点A重合，点F在AB上，让△EFG的边EF在AB上，点G在DC上，以每秒1个单位的速度沿着AB方向向右运动，如图②，点F与点B重合时停止运动，设运动时间为t秒．
如图，A点、B点分别表示小岛码头、海岸码头的位置，离B点正东方向的7.00km处有一海岸瞭望塔C，又用经纬仪测出：A点分别在B点的北偏东57°处、在C点的东北方向．
如图△ABC三点的坐标分别为A（1，5），B（4，1），C（1，1）